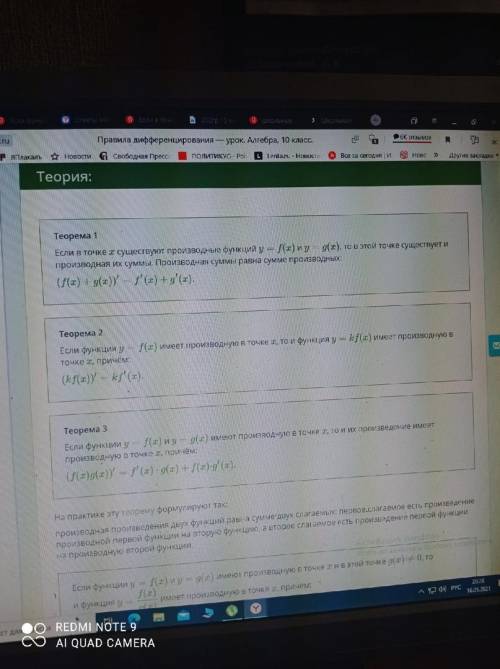
решить Теорема 1 Если в точке x существуют производные функций y=f(x) и y=g(x), то в этой точке существует и производная их суммы. Производная суммы равна сумме производных:

(f(x)+g(x))′=f′(x)+g′(x).

Теорема 2

Если функция y=f(x) имеет производную в точке x, то и функция y=kf(x) имеет производную в точке x, причём:

(kf(x))′=kf′(x).

Теорема 3

Если функции y=f(x) и y=g(x) имеют производную в точке x, то и их произведение имеет производную в точке x, причём:

(f(x)g(x))′=f′(x)⋅g(x)+f(x)⋅g′(x).

Гуленко    1   16.05.2021 20:34    0