Решить систему соотношений относительно множества Х и указать условия совместимости системы
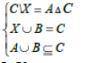
Другие вопросы по теме Математика
Популярные вопросы
- Грабеж, то есть открытое хищение чужого имущества, наказывается...
2 - Укажите предложение с причастным оборотом(знаки препинания не...
1 - Вставь пропущенных слова. уже в середине первого тысячелетия до...
2 - ответьте на вопросы по языку ((можно на )) 12 предложений или...
2 - Сделать программу в basic. в одномерном массиве с четным количеством...
2 - 7. укажите простую форму превосходной степени прилагательного:...
2 - Магазин делает пенсионерам скидку на определенное количество процентов...
3 - Определите, в каком варианте не пишется раздельно: а) купили машину...
1 - Антонова, получающая трудовую пенсию по случаю потери кормильца...
1 - Как обозначается ускорение в и измеряют...
2
Відповідь:
Покрокове пояснення:
Из уравнения А∪В⊆С следует, что и А и В есть подмножество С
Из Х∪В=С, что Х также есть подмножеством С и вместе с В даёт С, тесть Х есть дополнением В к С или Х⊆В, тогда В=С или Х и В пересекаются и полностью покрывают С . Тогда или А⊆Х , или они пересекаются, или нет
Учитывая 3 А ⊆С в правой части 1 уровня имеем АΔС=А\С∪С\А=С\А, поэтому С\Х=С\А, это может быть когда Х=А
Система совместима, когда Х=А⊆С
Несовместимы, когда Х и А не равны, не пересекаются