1. Математика
  2. Решить систему методом обратной

Решить систему методом обратной матрицы по формуле крамера или гаусса 4x-3y+2z+4=0 6x-2y+3z+1=0 5x-3y+2z+3=0

qwdv qwdv    1   06.09.2019 21:20    1

Ответы
Помощниица1 Помощниица1  06.10.2020 21:51
Метод Жордана-Гаусса:
\left[\begin{array}{ccc|c|c}4&-3&2&-4&-1\\6&-2&3&-1&\\5&-3&2&-3&\uparrow\end{array}\right]\ \textgreater \ \left[\begin{array}{ccc|c|c}-1&0&0&-1&*(-1)\\6&-2&3&-1&\\5&-3&2&-3&\end{array}\right]\ \textgreater \ \\\ \textgreater \ \left[\begin{array}{ccc|c|c}1&0&0&1&\downarrow\\6&-2&3&-1&-6\\5&-3&2&-3&-5\end{array}\right]\ \textgreater \ \left[\begin{array}{ccc|c|c}1&0&0&1&\\0&-2&3&-7&:(-2)\\0&-3&2&-8&\end{array}\right]\ \textgreater \ \\\ \textgreater \ \left[\begin{array}{ccc|c|c}1&0&0&1&\\0&1&-1,5&3,5&\downarrow\\0&-3&2&-8&3\end{array}\right]\ \textgreater \
\left[\begin{array}{ccc|c|c}1&0&0&1&\\0&1&-1,5&3,5&\\0&0&-2,5&2,5&:(-2,5)\end{array}\right]\ \textgreater \ \left[\begin{array}{ccc|c|c}1&0&0&1&\\0&1&-1,5&3,5&1,5\\0&0&1&-1&\uparrow\end{array}\right]\ \textgreater \ \\\ \textgreater \ \left[\begin{array}{ccc|c|c}1&0&0&1&\\0&1&0&2&\\0&0&1&-1&\end{array}\right]

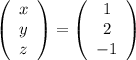
\left(\begin{array}{c}x\\y\\z\end{array}\right)= \left(\begin{array}{c}1\\2\\-1\end{array}\right)
ПОКАЗАТЬ ОТВЕТЫ
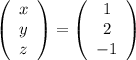
Другие вопросы по теме Математика
Vovavelchenko12 Vovavelchenko12  04.11.2020 12:22
1.20,21,35, 45,50, 90 сандарынан: а) 5-ке бөлінетін, b) 100-дин болингиштерин, c) 90 санының болингиштери болмайтын сандар...
катя5080 катя5080  04.11.2020 12:22
В саду росло 64 дерево из них 32 груши какую часть составили груши?​...
ятупик2 ятупик2  04.11.2020 12:22
КР СЕЙЧАС Паралелограм із сторонами 12см і 9см знайти площу якщо сума нерівних висот 14см ​...
dan5259oxnhwz dan5259oxnhwz  04.11.2020 12:22
Кто Добрый Сделать Правильно все задание)​...
7LoLiTa7 7LoLiTa7  04.11.2020 12:21
Используя цифры 4, 5, 6, составь двузначные числа. Найди количество четных и нечетных чисел. Количество четных чисел: .Количество нечетных чисел: . ​...
Maryyy100 Maryyy100  04.11.2020 12:20
4. Расставьте, не выполняя умножения, в по- рядке возрастания произведения:13×41, 16×48, 9×34, 3 × 12, 46× 54.​...
nrcsgt nrcsgt  04.11.2020 12:20
– (–(–7) + (–3)) – (–(–5) – 1 – (–8)).сколько​...
Tictax Tictax  04.11.2020 12:20
ОЧЕНЬ Знайдiть площу паралелограма зi сторонами 2см i 5см та кутом мiж ними 120 градусiв На Русском Найти площадь параллелограмма со сторонами 2см и 5 см и углом между ними 120 градусов...
холера663 холера663  04.11.2020 12:20
Какая часть квадрата закрашена?Запиши обыкновенную и десятичную дробь​...
varyatitova20 varyatitova20  04.11.2020 12:20
Заработная плата в месяц по трудовому договору между ООО «Ракета» и сотрудником Елистратом составляет сумму, после вычета из которой подоходного налога (13%) Елистрат получает на...

Популярные вопросы