Решить симметрическое уравнение с замены переменных
3x^4+2x^3+7x^2+2x+3=0
Другие вопросы по теме Математика
Популярные вопросы
- Підібрати синоними до слова сильный...
2 - Предложение со словом эстетитический...
1 - Как решить вот эти дроби 7/14+2/7...
1 - Ученик прочитал 36 страниц что составило 0.75 всей книги. Сколько страниц в книге...
1 - а то за лето всё забыла=)там нужен только Б...
1 - перепиши числа из разрядной таблицы в строку или наоборот Выдели самое большое...
2 - ЖАЗЫЛЫМ 11-тапсырма. Сөздердегі түсіп қалған әріптердің қандай ды-бысты таңбалайтынын...
2 - Как озаглавить текст про первый полёт в космос более грамматично?...
3 - 10 байт = бит 15кб =байт1 мб = кб1 гб = мб1 тб = гб1 пб = тб1 эб =пб1 зб = эб1...
2 - 3 * (- 2) + (- 3) (- 4) – (- 5) * 7; вычислить...
3
Пусть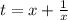 ;
; 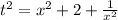 ;
; 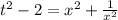
ответ: Нет корней