решить Распишите все подробнее Задание 1. . Установите соответствие между графиком функции и характером точки x=a
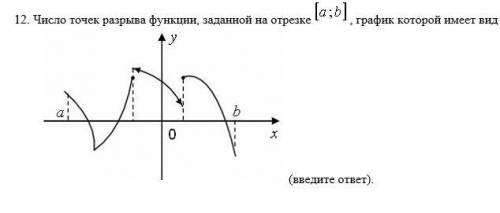
Задание 2. . Число точек разрыва функции, заданной на отрезке [a;b] график которой имеет вид

У меня не погружается фото, можешь написать что там написано, у меня интернет слабый

Задание 1. Нам дан график функции и необходимо установить соответствие между графиком и характером точки x=a.

Для выполнения этого задания мы должны различать четыре возможных варианта:

1. Если график функции пересекает ось x в точке a, то это означает, что функция имеет корень в точке x=a. Корень функции - это значение переменной x, при котором значение функции равно нулю. Графически это выглядит как пересечение графика с осью x.

2. Если график функции касается, но не пересекает ось x в точке a, то это означает, что функция имеет корень кратности больше 1. Корень функции кратности n - это значение переменной x, при котором значение функции и ее первой n-1 производных равны нулю, а n-я производная отлична от нуля. Графически это выглядит как касание графика к оси x.

3. Если график функции пересекает ось x в точке a и меняет свой характер, например, с возрастания на убывание или наоборот, то это означает, что в точке x=a происходит разрыв второго рода. Разрыв второго рода происходит, когда значение функции в точке x=a стремится к бесконечности или не существует.

4. Если график функции проходит через вершину параболы и не пересекает ось x в точке a, то это означает, что значение функции в точке x=a является локальным минимумом или максимумом. Локальный минимум или максимум функции - это значение функции, которое является наименьшим (наибольшим) среди значений функции в некоторой окрестности данной точки.

Задание 2. Нам дан график функции на отрезке [a;b]. Необходимо определить количество точек разрыва функции.

Для выполнения этого задания мы должны обратить внимание на особенности графика функции. На графике данной функции видно, что есть точки, где график функции имеет положительную или отрицательную бесконечность. Такие точки являются точками разрыва функции.

Анализируя данное изображение графика функции, мы видим три такие точки: одна на интервале (a,b) и две на концах интервала [a;b]. Следовательно, количество точек разрыва функции на отрезке [a;b] равно трем.

Таким образом, мы подробно рассмотрели решение задания 1, установили соответствие между графиком функции и характером точки x=a, а также рассмотрели решение задания 2 и определили количество точек разрыва функции на отрезке [a;b].