решить примеры решить примеры ">

№1     х=3, у=4 или х=4, у=3

х²+у²=25

х+у=7

х=7-у, подставляем данное выражение в первое уравнение и решаем

(7-у)²+у²=25

49-14у+у²+у²=25

2у²-14у+24=0

у²-7у+12=0

Находим дискриминант

D=7²-4·1·12=49-48=1, значит будет два корня

=(7-)/2=6/2=3

=(7+)/2=8/2=4

теперь находим значения х

=7-у=7-3=4

=7-у=7-4=3

№2     х=1, у=2

3х²+у²=7

х²+2у²=9

домножаем каждый член первого уравнения на (-2)

-6х²-2у²=-14

х²+2у²=9

складываем почленно левую и прав. части уравнений системы уравнений

-5х²=-5

5х²=5

х²=1

х=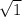=1  теперь находим у

у²=7-3х²=7-3=4

у=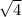=2

№3      х=2, у=3

2х-у=1

3х+2у=12

домножаем каждый член первого уравнения на 2

4х-2у=2

3х+2у=12

складываем почленно левую и прав. части уравнений системы уравнений

7х=14

х=14÷7=2

находим значение у

у=2х-1=4-1=3

№4    длина 6 см, ширина 3 см

пусть а см - длина прямоугольника, b см - ширина

составляем систему уравнений

а²+b²=45

(а+b)·2=18

упрощаем

а²+b²=45

а+b=9         то есть b=9-а  и подставляем в первое уравнение

а²+(9-а)²=45   и решаем

а²+81-18а+а²=45

2а²-18а+36=0           сокращаем на 2

а²-9а+18=0

находим дискриминант

D=81-4·18=81-72=9  

теперь находим по формуле корней длину прямоугольника

=(9+)/2=(9+3)/2=6

=(9-)/2=6/2=3

находим ширину прямоугольника

=9-a=9-6=3

=9-3=6

по смыслу подходит длина 6 см, тогда ширина 3 см

№5   длина 12 см, ширина 5

пусть а см - длина прямоугольника, b см - ширина

так как диагональ - это гипотенуза в треугольнике, где катеты это стороны прямоугольника

составляем систему уравнений

(а+b)·2=34

a²+b²=13²  

то есть

а+b=17

a²+b²=169

выражаем b=17-a и подставляем во второе уравнение

а²+(17-а)²=169   и решаем

а²+289-34а+а²=169

2а²-34а+120=0   сокращаем на 2

а²-17а+60=0

находим дискриминант

D=17²-4·60=289-240=49  D больше 0, значит два корня

теперь находим по формуле корней длину прямоугольника

=(17-)/2=(17-7)/2=5

=(17+)/2=(17+7)/2=12

теперь находим ширину

=17-a=17-5=12

=17-a=17-12=5

по смыслу подходит 12 см - длина, тогда 5 см - ширина

Пошаговое объяснение: