1. Математика
  2. Решить прикладные задачи

Решить прикладные задачи с использованием интегрального исчисления 55 б) вычислить площадь фигуры, ограниченную заданными линиями:
у = х+2, х = 2, х = 4.

if395478 if395478    1   30.12.2021 20:55    0

Ответы
кузя177 кузя177  30.12.2021 22:00

Это трапеция. См. рисунок ниже.

Решение.

S=\int\limits^4_2 {(x+2)} \, dx =(\frac{x^{2} }{2}+2x) |^4_2=(\frac{4^{2} }{2} +2*4)-(\frac{2^2}{2}+2*2) =16-6=10

ответ:  S=10


Решить прикладные задачи с использованием интегрального исчисления 55 б) вычислить площадь фигуры, о
ПОКАЗАТЬ ОТВЕТЫ
Chakachoco Chakachoco  30.12.2021 22:00

\int\limits^4_2 ({x+2)} \, dx=(\frac{4^2}{2}+2*4)-(\frac{2^2}{2} +2*2)=(\frac{16}{2} +8)-(\frac{4}{2} +4)=(8+8)-(2+4)=16-6=10

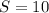
ответ: S=10

Пошаговое объяснение:

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
  10.09.2019 00:10
Расстояние между поселками 24 км . из них одноврменно на встречу друг другу вышли 2 человека и встретились через 4 часа найдите скорость второго путника если скорость...
ROLFRUTIN ROLFRUTIN  10.09.2019 00:10
Косцы в первый день скосили половину луга и ещё 2 га,во второй день-сначала 25% оставшейся части, а когда передохнули,осилили и последние 6 га.найдите площадь луга...
aaaaaalina1yuin aaaaaalina1yuin  10.09.2019 00:10
19. радиус основания конуса равен 2 см. осевым сечением является прямоугольный треугольник. найти площадь осевого сечения....
rotsib rotsib  10.09.2019 00:10
При каком значении х верно равенство х/4=72/a,где ведётся a наибольшим двузначным числом, краным 4...
matanya281 matanya281  10.09.2019 00:10
Твір на тему що таке справедливість...
karkhachatryan karkhachatryan  10.09.2019 00:10
Радиус основания конуса равен 2 см. осевым сечением является прямоугольный треугольник. найти площадь осевого сечения....
lyazkaiman0309 lyazkaiman0309  10.09.2019 00:10
На xxii олимпийских играх в м оскве(1980г.) спортсмены 195 медалей из них 126 золотых и бронзовых ,149 золотых и серебряных. сколько золотых ,серебряных и бронзовых...
ulianadmytryk1 ulianadmytryk1  10.09.2019 00:10
Запишите частное наибольшего четырехзначного числа и наибольшего четного двухзначного числа. представьте частное в виде обыкновенной дроби. выделите целую часть...
toshakotik toshakotik  10.09.2019 00:10
Найдите значение выражения 9/x - 9/5x при x = -2 ответ: -3,6 дайте полное решение и объясните все подробно...
kcatuscha2016 kcatuscha2016  10.09.2019 00:10
Мастерской шили восемь одинаковых пальто и несколько костюмов и израсходовали 61 м материи. на каждый пальто расходуются 3 м 25 см матери, на каждый костюм на 25...

Популярные вопросы