Решить поэтапно избегая нуля при базовом подставлении значений предела.
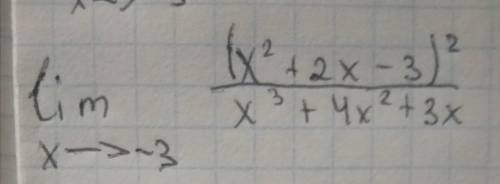
Другие вопросы по теме Математика
Популярные вопросы
- Как находится периметр равностороннего треугольника? заранее : )...
2 - Составьте блок-схему и опишите на языке программирования алгоритм...
2 - Правопис прислівника : швидкуруч. як правильно писати нашвидкуруч...
3 - 1.в древней греции,говорят,была демократия. и все решали голосованием....
1 - Крошка ру хочет пройти из комнаты а в комнату б. через какое наименьшее...
2 - Синоніми к слову помітивши,визирнуло, крихітну...
3 - Δabс,∠c=90° ∠a=45°,ac=6(см) найти: bc...
2 - Два пешехода шли с одинаковой скоростью. один км, а другой 12 км....
1 - Найдите шестой член прогресси (bn) , если b1=3 , g=1\3...
1 - Чем похожи герои рассказов последний лист и дары волхвов?...
3
ответ: 0.
Пошаговое объяснение:
Подстановка x=-3 приводит к неопределённости 0/0. Для её уничтожения заметим, что x²+2*x-3=(x+3)*(x-1), а x³+4*x²+3*x=x*(x+1)*(x+3). После этого числитель и знаменатель дроби можно сократить на (x+3) и мы получим дробь (x+3)*(x-1)/[x*(x+1)]. При x⇒-3 числитель этой дроби стремится к 0, а знаменатель - к 6, поэтому искомый предел равен 0/6=0.