Математика: решить номер 6 и номер большое!

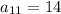
6. Выгоднее производить модель «В», следует установить при продаже цену в $125.7. Пошаговое объяснение:6. Оценим прибыльность производства и продажи каждой из моделей телефона.Затраты на производство модели «А» составляют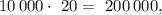 а на производство модели «В» —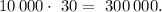 Так как планируется продать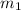 смартфонов модели «А» по цене 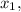выручка от их продаж составит Аналогично для модели «В» —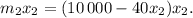 Прибыль от продаж равна выручке минус затраты на производство. Таким образом, прибыль от модели «А» составляета от модели «В» — Оценим...

решить номер 6 и номер большое!

Ответы

357853 09.08.2022 06:00

6. Выгоднее производить модель «В», следует установить при продаже цену в $125.

7. $a_{11}=14$

Пошаговое объяснение:

6. Оценим прибыльность производства и продажи каждой из моделей телефона.

Затраты на производство модели «А» составляют $10\,000 \cdot \ 20 = \ 200\,000,$ а на производство модели «В» — $10\,000 \cdot \ 30 = \ 300\,000.$

Так как планируется продать ${m_1}$ смартфонов модели «А» по цене ${x_1},$ выручка от их продаж составит

${m_1}{x_1} = (10\,000 - 50{x_1}){x_1}.$

Аналогично для модели «В» — ${m_2}{x_2} = (10\,000 - 40{x_2}){x_2}.$

Прибыль от продаж равна выручке минус затраты на производство.

Таким образом, прибыль от модели «А» составляет

$(10\,000 - 50{x_1}){x_1} - 200\,000,$

а от модели «В» —

$(10\,000 - 40{x_2}){x_2} - 300\,000.$

Оценим прибыль для модели «А»:

$(10\,000 - 50{x_1}){x_1} - 200\,000 = 10\,000{x_1} - 50x_1^2 - 200\,000.$

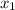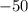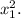Полученное уравнение представляет собой квадратный трехчлен относительно переменной ${x_1}$ с коэффициентом при x_1^2. Это значит, что график такого уравнения будет параболой с ветками, направленными вниз, максимальное значение такой параболы достигается в ее вершине, координаты которой находятся по формуле

${x_B} = - \displaystyle\frac{b}{{2a}} = - \displaystyle\frac{{10\,000}}{{2( - 50)}} = 100.$

Подставляя найденное значение в уравнение прибыли, оценим ее размер:

$10\,000 \cdot 100 - 50 \cdot {100^2} - 200\,000 = {\rm{300}}\,{\rm{000}}{\rm{.}}$

Значит если продавать смартфоны модели «А» по цене $100 за единицу, прибыль составит $300 тыс.

Аналогично оцениваем прибыль для модели «В»:

$(10\,000 - 40{x_2}){x_2} - 300\,000 = 10\,000{x_2} - 40x_2^2 - 300\,000,$

${x_B} = - \displaystyle\frac{{10\,000}}{{2 \cdot ( - 40)}} = 125,$

значение функции при этом значении аргумента равно

$10\,000 \cdot 125 - 40 \cdot {125^2} - 300\,000 = 325\,000.$

Значит если продавать смартфоны модели «В» по цене $125 за единицу, прибыль составит $325 тыс.

Получается, производить смартфоны модели «В» выгоднее.

7. Используем формулу общего члена прогрессии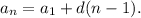 a_n=a_1+d(n-1).

$\left\{ \begin{array}{l}\displaystyle\frac{{{a_3}}}{{{a_{10 = \displaystyle\frac{{11}}{{32}},\\{a_4} + {a_8} = 16;\end{array} \right.$

$\left\{ \begin{array}{l}\displaystyle\frac{{{a_1} + 2d}}{{{a_1} + 9d}} = \displaystyle\frac{{11}}{{32}},\\{a_1} + 3d + {a_1} + 7d = 16.\end{array} \right.$

Из второго уравнения

$2{a_1} + 10d = 16, {a_1} + 5d = 8, {a_1} = 8 - 5d.$

Подставляя найденное значение в первое уравнение, имеем:

$\displaystyle\frac{{8 - 5d + 2d}}{{8 - 5d + 9d}} = \displaystyle\frac{{11}}{{32}};displaystyle\frac{{8 - 3d}}{{8 + 4d}} = \displaystyle\frac{{11}}{{32}};32(8 - 3d) = 11(8 + 4d);256 - 96d = 88 + 44d;96d + 44d = 256 - 88;140d = 168;d = \displaystyle\frac{{168}}{{140}} = \displaystyle\frac{6}{5}.$