решить неравенство!
подробно.

Другие вопросы по теме Математика
Популярные вопросы
- Сколько всего единиц в 6десятках? 1)60 2)6 3)0...
2 - Сделать грамматические . 1.помню застигнувшую нас в дороге грозу. 2.я сидел с матерью...
2 - Рассчитайте массу 1 моля оксида фосфора (5)...
1 - От пристани а до пристани в лодка плыла по течению реки 3,5 ч.на обратный путь...
1 - 1)sin2b-sin2b*cos2b=? 2)cos4b+cos2b*sin2b=? 3)tg2b*ctg2b-cos2b=?...
2 - Сторона основи правильної чотирикутної піраміди = 3см, а апофема - 5 см. знайдіть...
1 - Замени два действия одним *18 : 6 ; 2) *15 : 3; 3) : 7*28; 4) : 11 *110...
2 - Выполните действия (18 - 10 18\35) - (3 9\28 + 2 3\20) =...
2 - Переведите следующие предложения: 1. мы не разместим у них заказ, если они не снизят...
1 - Мини сочинение на тему каким бы я хотел (а) видеть окружающий меня мир...
1
x∈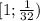 ∪
∪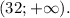
Пошаговое объяснение:
Преобразовываем выражение:
Находим нули каждого множителя:
По методу интервалов решением неравенства является промежуток: