решить неравенство log2(x-14)-1/2log2(3x-26)>1
Другие вопросы по теме Математика
Популярные вопросы
- Вкниге было прочитано 234 страницы что составляет 36% от книги сколько...
3 - Президент сша у.тафт в очередном послании конгрессу страны (декабрь...
3 - Разложите на множители: 3a+6b; 12m-16n; 10ck-15cp; 8ax+8a; 5b-25bc;...
3 - Скорость самолета 500 км/ч. сколько километров он пролетит: а) за...
1 - Какой город лишний лиссабон кордовы гранаде авиньон севилья...
1 - Найдите площадь равнобедренной трапеции ,если ее основание равно 4...
1 - Увити было 90 гвоздей. на ремонт мебели у него ушло 7/18 всего количества...
1 - Президент мексики в. карранса в одном из выступлений (сентябрь 1915...
2 - (напишите краткую запись) масса одного ящика с яблоками 10 кг,а с...
2 - Имя существительное. вариант№1. 1.выбери верное утверждение. 1) имя...
1
Пошаговое объяснение:
ОДЗ:
Вычитаемое перебросим вправо со знаком + и умножим обе части на 2:
По свойствам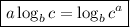 ,
, 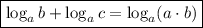 преобразуем обе части:
преобразуем обе части:
Логарифмы опускаем, знак сохраняем, так как основание 2 > 1.
Нули левой части удобно найти по теореме Виета:
Записываем неравенство в виде , решаем методом интервалов (вложение) и получаем, что
, решаем методом интервалов (вложение) и получаем, что 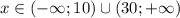 . Вспоминаем, что по ОДЗ x > 14 - значит, ответом служит только второй интервал.
. Вспоминаем, что по ОДЗ x > 14 - значит, ответом служит только второй интервал.
ОТВЕТ: (30; +∞)