1. Математика
  2. решить неопределённые интегралы,

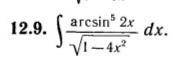
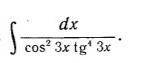
решить неопределённые интегралы, обязательно с подробным интегрированием


решить неопределённые интегралы, обязательно с подробным интегрированием
решить неопределённые интегралы, обязательно с подробным интегрированием
решить неопределённые интегралы, обязательно с подробным интегрированием

djsxv djsxv    2   09.01.2021 08:08    0

Ответы
яло203 яло203  12.02.2021 22:41

1.

\int\limits \frac{dx}{(x + 1) \sqrt[3]{ ln(x + 1) } } \\

1/(x+1) - это производная логарифма, заносим под знак дифференциала

\int\limits \frac{1}{x + 1} \times \frac{dx}{ \sqrt[3]{ ln(x + 1) } } = \int\limits \frac{d ln(x + 1)) }{ {ln}^{ \frac{1}{3} }(x + 1) } = \\ = \frac{ {ln}^{ \frac{2}{3} } (x + 1)}{ \frac{2}{3} } + C = \frac{3}{2} \sqrt[3]{ {ln}^{2} (x + 1)} + C

2.

\int\limits \frac{ {arcsin}^{5} (2x)}{ \sqrt{1 - 4 {x}^{2} } } dx \\

1/(1-4x^2)^(1/2)) - это производная акрсинуса. Заносим под дифференциал, но сначала добавим в него двойку, так как функция сложная.

\frac{1}{2} \int\limits \frac{ {arcsin}^{5}(2x)d(2x) }{ \sqrt{1 - 4 {x}^{2} } } = \\ = \frac{1}{2} \int\limits {arcsin}^{5} (2x)d(arcsin(2x)) = \\ = \frac{1}{2} \frac{ {arcsin}^{6}(2x) }{6} + C = \frac{ {arcsin}^{6}(2x) }{12} + C

3.

\int\limits \frac{dx}{ { \cos }^{2}(3x) {tg}^{4} (3x) } \\

1/cos^2x - производная тангенса. Заносим под дифференциал, но сначала добавим 3.

\frac{1}{3} \int\limits \frac{1}{ { \cos}^{2}(3x) } \times \frac{d(3x)}{ {tg}^{4}(3x) } = \\ = \frac{1}{3} \int\limits {tg}^{ - 4} (3x)d(tg3x) = \frac{1}{3} \times \frac{ {tg}^{ - 3} 3x}{( - 3)} + C = \\ = - \frac{1}{9 {tg}^{3}(3x) } + C

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
axon11kot axon11kot  02.02.2021 16:37
У меня ещё куча уроков не сделано можете с математикой ​...
Sfdfgc Sfdfgc  02.02.2021 16:37
Суммативное оценивание по естествознанию за 3 четверть 3 класс ФиЗадание 1 [4]181.1. Слой почвы в 18 см вода сможет смыть за 500 тысяч лет, на лугу -за3225 лет, атам, где нет растений...
noname1372321 noname1372321  02.02.2021 16:37
С тем что я обвела Можно быстр​...
cangelina2025 cangelina2025  02.02.2021 16:37
8 Вычисли, записывая по действиям, 13 440 : 32 7+7 1238573 - 4 422 2 - 1 5677924 - 5 832 : 2 - 3 822509 - 603 - 999 999 : 11 + 3982(8 535 - 1579) : 4 + 3 456(12 789 - 8845) : 4 + 26...
liza20038333 liza20038333  02.02.2021 16:37
Если трехзначное число 52m делится на 5 без остатка, то найдите сумму цифр, которые можно поставить вместо т.​...
israelyan87 israelyan87  02.02.2021 16:38
Длина прямоугольника 16 cm, ширина - 5 ст. Стороны этого прямоугольника уменьшили на 5 смНайди периметрполученногоугольника.5cm.прямоугольника только с условием например Дано:АВСД...
anisinivan09p08i87 anisinivan09p08i87  02.02.2021 16:38
1) Запишите формулу периметра прямоугольника (длины сторон обо- значьте буквами а и b).2) Запишите формулу площади прямоугольника.3) Вычислите периметр и площадь прямоугольника, если...
кроп1 кроп1  02.02.2021 16:38
запишіть у вигляді неправильного дробу число 1) 2 1/8; 2) 4 3/11; 3) 6 15/40; 4) 25 3/4;...
bpanvk1 bpanvk1  02.02.2021 16:38
ОТВЕТЬТЕ! КАК СДЕЛАТЬ ОТВЕТ ЛУЧШИМ ?​...
dcherbaev7771 dcherbaev7771  02.02.2021 16:39
даю если будет не правильно бан​...

Популярные вопросы