Решить : напишите уравнение параболы, проходящей через три точки (x,y):
(1,2), (3,10), (5,1)

Пошаговое объяснение:

Уравнение параболы в общем виде записывается следующим образом:

где , 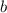и -- коэффициенты, которые нам необходимо найти.

Подставим известные нам точки в уравнение параболы и составим систему из трёх уравнений:

Эту систему можно решать по-разному, дело вкуса. Даю простейшее решение с выражением каждого неизвестного по-очереди.

Умножим второе уравнение на 2 и вычтем из третьего второе, чтобы избавиться от :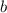

Отсюда видно, что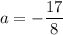 , 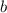получаем из второго уравнения, а из первого:

Таким образом,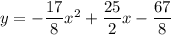 - уравнение нашей параболы.