Решить матричное уравнение
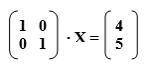
Другие вопросы по теме Математика
Популярные вопросы
- Что такое род молю и ещё что такое община,племя...
3 - Вариант 6. 1.диагонали прямоугольника авсд пересекаются в точке о, угол аов...
1 - По за 3класс например периметр квадрата равен 28 см. чему равна его сторона?...
1 - Длина спортивной площадки прямоугольной формы равна 400м а ширина 200м. найди...
1 - Составить устный рассказ: «воздействие музыки на человека, её взаимосвязи с...
2 - За три дня рабочий изготовил 208 деталей. в первый день он выполнил норму, во...
1 - Сумма чисел 26, а 19% другого другого числа вместе составляют 2,5 . найдите...
1 - «да» или «нет»? определите, являются ли верными следующие суждения вопрос №...
1 - Найдите четные только четные 1 3/5 2 5/6 3 5/7 5 4/9 8 1/8 13 1/10 13 7/15 17...
2 - Как бцдет по 4 верхних и 5 нижних ящиков?...
2
Пошаговое объяснение:
А*Х=В
определитель матрицы А
∆ = 1*1 - 0*0 = 1
т.к A невырожденная матрица, то существует обратная матрица A⁻¹. Умножим слева обе части уравнения на A⁻¹
A⁻¹*A*X = A⁻¹*B,
тогда получим E·X = A⁻¹*B, или X = A⁻¹*B.
Найдем обратную матрицу A⁻¹.