1. Математика
  2. Решить .лучше с подробным расписание

Решить .лучше с подробным расписание решения

Mihail568 Mihail568    1   28.10.2019 01:18    0

Ответы
dilnoza55 dilnoza55  10.10.2020 09:57

1) \frac{2}{3}\sqrt{x^3+5}+C

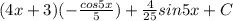
2) (4x+3)(-\frac{cos5x}{5})+\frac{4}{25} sin5x+C

Пошаговое объяснение:

1)

\int {\frac{x^2dx}{\sqrt{x^3+5}}}= \frac{1}{3}\int {\frac{d(x^3+5)}{\sqrt{x^3+5}}}=\frac{1}{3}\int {d(x^3+5)(x^3+5)^{-\frac{1}{2}}}=\frac{2}{3}\sqrt{x^3+5}+C

2)

\int {(4x+3)sin5xdx}

Для нахождения интеграла нужно использовать формулу интегрирования по частям:

\int {udv}=uv- \int{vdu}

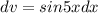
где u=4x+3 , dv=sin5xdx

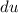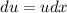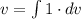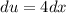Нужно найти дифференциал du, используя du=udx, вычислить v при v=\int1\cdot dv и подставить du=4dx и v=\frac{-cos5x}{5}

\int {(4x+3)sin5xdx}=(4x+3)(-\frac{cos5x}{5})-\int {-\frac{cos5x}{5}4dx}=(4x+3)(-\frac{cos5x}{5})+\frac{4}{5} \int {cos5xdx}=(4x+3)(-\frac{cos5x}{5})+\frac{4}{5}\cdot \frac{1}{5} \int {cos5xd(5x)}=(4x+3)(-\frac{cos5x}{5})+\frac{4}{25} sin5x+C

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
imail91 imail91  02.12.2020 13:32
50 мм 32 ММ103 ММБерілген параллелепипедтен 100 есе кемтіктөртбұрышты параллелепипедтің​...
Тeлeпузік Тeлeпузік  02.12.2020 13:32
дам 30б 1. Требуется смешать 3 части песка и 2 части цемента. Сколько цемента и песка нужно взять отдельно, чтобы получить 30 кг смеси?2. Для компота купили 1800 г сухофруктов....
markus10024 markus10024  02.12.2020 13:32
Установи соответствие между фразеологизмом и его значением. Надувать губыХорошенько запоминатьМотать на усСразу видно, ясно по внешнему видучеловекаНа лбу написаноЗапутывать,...
likarabigba likarabigba  02.12.2020 13:32
при каком значении n верно равенство 1)3n=9 2)128=2n 3)(2²)n=16 4)(3n)²=81 кто решит и подпишусь дам корону и поставлю лайк​...
navaxa navaxa  02.12.2020 13:32
на пошиття 5 суконь витратили 12 м тканини. скільки потрібно тканини щоб пошити 16 суконь​...
dashoostik dashoostik  02.12.2020 13:32
Прослушай рассказ плохо . Определи, отражают ли данные слова основную информацию текста...
nastyaborisova13 nastyaborisova13  02.12.2020 13:32
Самостоятельная работа №1 «Производная суммы и разности»...
Stacool220 Stacool220  02.12.2020 13:32
2/3×6/7=4/7×21/40=37/32×8/9=5\11×22/25=8/35×5/12=...
SuPeRGaMeRDGRST SuPeRGaMeRDGRST  02.12.2020 13:32
Максим потратил x рублей,а Лена-на 10рублей больше.Сколько рублей потратили дети?а)10x;б)2x+10;в)x+10;г)12x​...
ViWell ViWell  02.12.2020 13:32
Постройте график функции у=-2х4 и ещё один у=5/х3...

Популярные вопросы