Решить логарифмическое неравенство.
Ответы
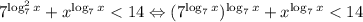 ; Используя основное логарифмическое тождество, получим:
; Используя основное логарифмическое тождество, получим: 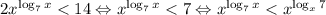 ; После этого введем замену:
; После этого введем замену: 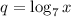 ; Тогда:
; Тогда:  ; Обратно к замене:
; Обратно к замене: 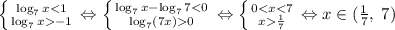
Другие вопросы по теме Математика
Популярные вопросы
- Выпишите из данного отрывка глаголы будущего времени По какой...
3 - A (4; 14; 2) b (2; 7; -1)c (0; 0 ;3)d (-6 ;-21; 3) Найти колинеарность...
3 - Нужно составить тонкие и толстые вопросы на 11 главу из Сказки...
3 - 4.Мир сатирической сказки М.Е. Салтыкова-Щедрина. Повесть о том,...
1 - Высота прямоугольного параллелепипеда 5, длины сторон основания...
1 - Определи, какой эпизод понять, что молодое поколение стремится...
2 - Какое же открытие совершил А.Н.Островский?...
2 - Найдите объём и площади поверхности тел изображённых на рисование...
3 - Vocabulary Choose the correct item. 1 There are many famous landmarks/cabs...
3 - В стране Б численность рабочей силы в предыдущем году составила...
2