Решить коши. 2yy''=(y')^2, y(1)=0, y'(1)=1
Другие вопросы по теме Математика
Популярные вопросы
- 2+3х-2х^2 больше или ровно 0 решите !...
3 - Определить ускорение, которое приобретает мяч массой 0,5 кг под...
2 - Составте схемы строения атомов. электроной форму ячейки для валентного...
3 - Докажите что при любом натуральном числе x значение выражения...
1 - Написать термины: вода- ; стакан- ;...
3 - Решить скажите как записать такую по действиям такая: 1. 7 значный...
2 - Изобразите какую нибудь фигуру и заукрасьте. ее часть которая...
1 - Назовите 2-3 знакомых вам рассказа, 1-2 повести и романа. к какому...
1 - Какое главное событие книжки витя малеев в школе и дома...
2 - Представьте в виде произведения выражение: ab-ac+bd-cd...
1
Это уравнение вида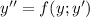 . Для решения такого уравнения нужно вводить новую замену
. Для решения такого уравнения нужно вводить новую замену  , тогда
, тогда 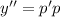
Это дифференциальное уравнение первого порядка разрешенной относительно производной, уравнение с разделяющимися переменными.
Сделав обратную замену: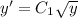
Получили общий интеграл. Теперь нужно найти частное решение, подставив начальные условия: y(1)=0 и y'(1)=1.