решить интеграл: 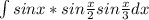 ответ должен выйти:
ответ должен выйти: 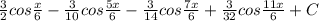
Другие вопросы по теме Математика
Популярные вопросы
- Выберите верные утверждения: 1) работа силы тяжести всегда отрицательная...
1 - Мопед, скорость которого 18 км/ч и трактор, скорость которого 36 км/ч...
3 - Какой вид и отряд у иксовидного клеща?...
3 - Сочинение надо ну сочинение на тему полицейского...
3 - Определите род следующих существительных, подобрав к ним прилагательные....
1 - Вкаком году началась 2 мировая война! ?...
1 - Надземная часть состоит из подзменая часть растения образована корневой...
1 - Ввыражении 1? 2? 3? 4? 5? 6? 7? 8? 9 вместо каждого из знака ? поставьте...
1 - Напишите 1.902894e16 нормальным языком. допустим 186363829...
1 - Выпишите 10 предложений состоящих из причастных оборотов в деепричастных...
1
Пошаговое объяснение: