Решить интеграл от 0 до пи/4 (sinx-cosx)/(cosx+sinx)^3
Ответы
Сделаем замену переменной 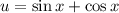 , тогда
, тогда 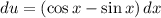 . u как функция от x на промежутке интегрирования монотонно возрастает от
. u как функция от x на промежутке интегрирования монотонно возрастает от 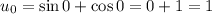 до
до 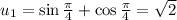
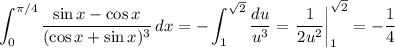
ПОКАЗАТЬ ОТВЕТЫ
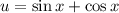 , тогда
, тогда 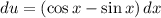 . u как функция от x на промежутке интегрирования монотонно возрастает от
. u как функция от x на промежутке интегрирования монотонно возрастает от 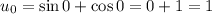 до
до 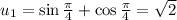
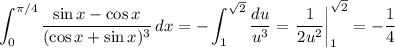
Другие вопросы по теме Математика
Популярные вопросы
- Міні твір чи важко бути говорющею рибою 10 надо...
3 - Кому живется плохой в город n? нужна это по рассказу ревизор...
2 - Добрый день. 1.иван-царевич нашел лягушку. 2.какими красками...
1 - 25 б. решить уравнение : 1) x-3 целых 8: пятнадцатых=4 целых...
2 - Какую роль играла винодельческая отрасль в каждого крестьянского...
1 - Решите производную f(x)=-1/2x^3 + x^3/4...
3 - Три мандарини розділили порівну між пятьма дітьми яку частину...
3 - Ученики рассматривают карту тульской области, отвечают на вопросы...
3 - Ондық бөлшекті кему ретімен орналастырғанда бірінші ондық бөлшекті...
2 - Write an email to your friend about your typical school day routine...
2