решить Интеграл. Не нужно брать из интернета и Photomath решения.
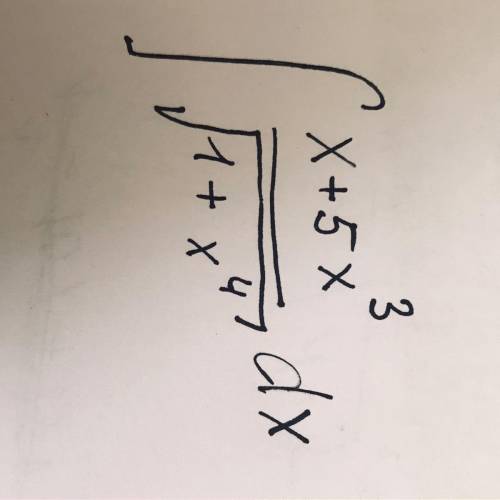
Другие вопросы по теме Математика
Популярные вопросы
- Переведите на 1.взять: листок бумаги ножницы цветные карандаши нитку и иголку...
1 - Напишите сравнительную характеристику 2 подруг...
1 - Решить ученик прочитал 21 страницу что составило три седьмых всей книги.сколько...
3 - А)78,9*10= б)8,01: 100= в)75,4*100000= г)48,1: 10000= д)1,3*0,001= е)45,7: 0,0001=...
3 - Вставь пропущеные буквы поэтниколай старшинов представля..т поколение , в страшн..й...
3 - Как определить предложения в present simple! ! заранее )...
2 - Найдите острые углы прямоугольного треугольника, если один из них на 38 градусов...
1 - Даны числа 3/2,2 1/4,4 2/3,6/5,31/6,2 5/8,3 1/2 выпишите числа заключенные между...
3 - 2,9а-2,3а+1,4а а=4,32 это уравнение...
1 - 1. связь в хлориде натрия, азота и метане соответственно 1) ковалентная неполярная,...
2
решение на фотографии.
Пошаговое объяснение: