Решить интеграл на рисунке
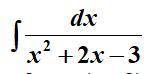
Другие вопросы по теме Математика
Популярные вопросы
- При каких значениях с(це) уравнение 2х^2-4х+с=0 не имеет корней?...
2 - 100 ! ! ! два круга, центры которых расположены по разные стороны...
3 - 1)(x-2)^2-(x-7)(7+x) 2)(10+x)(x-+3)^2 3)(9-x)(x+-7)^2 4)(3+x)^2-(x-3)^2...
2 - Бездомный зарабатывает 10 рублей в 40 секунд, он хочет простоять...
3 - Словосочетание со словом осине в д. п....
1 - Установи порядок действия. и вычесли.70-8×8×1= / 55÷55+6×6=/ 5×8-40÷1=/...
2 - Васе задано решить по и .в первый день он решил 1/15 всех по и 1/25...
3 - За 7 часов велосипедист проехал106.3/4 км.какое расстояние он проедет...
1 - Решите 5 номеров 15б. -8(y-1)(y+5) (3a+5)(3a+6)+30...
2 - Мүсінші əңгіме құру керек (7-8 сөйлем)...
3
Пошаговое объяснение:
Требуется решить интеграл.
В знаменателе выделим полный квадрат:
Используем формулу:
Получим: