решить эту задачу Sin(π/4-a) -√2/2sin a, cos a=0, 5
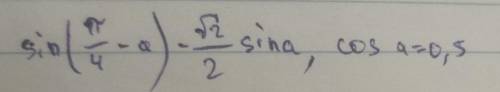
Другие вопросы по теме Математика
Популярные вопросы
- Изменить на пасивный голос:The cat has drunk the medicine....
2 - В июле планируется взять кредит в банке на целое число миллионов...
2 - Буржуазные революции в Австрии и Пруссии а) причины и предпосылки;...
2 - 6•. Сторона правильного трикутника, вписаного в коло, дорівнює 12...
1 - 3) Дан рекурсивный алгоритм: def F(n): print(n) ) if n 1: print...
2 - До іть ів всесвітня історія. Яке об єднання було перетворене у Світову...
3 - Можете , написать все цитаты Конфуция о деньгах , которые знаете...
1 - ОЧЕНЬ Порівняйте зміни у розвитку промисловості в Надніпрянській...
2 - 3. На рисунку 2 КМ = MN, ND = DE. Доведіть, що прямі КМ і DE паралельн...
1 - Составьте и запишите предложения по данным схемам. [О, …] […, О]...
2
Пошаговое объяснение:
Sin(π/4-a) -√2/2sina, cos a=0, 5;
Sin(π/4-a) -√2/2sina=sin(π/4)cosa-cos(π/4)sina-√2/2sina=
=√2/2cosa-√2/2sina-√2/2sina=√2/2cosa-√2sina=√2/2*(1/2)-√2sina=√2/2*(1/2)-√2(√3/2)=√2/4-√(3/2)
cos a=0, 5 to sina=√3/2 0<a<π/2
ответ: √2/2 ( 0,5 - √3 ) .
Пошаговое объяснение:
cosα = 0,5 ; sinα = √ ( 1 - cos²α ) = √ ( 1 - 0,5²) = √0,75 = 0,5√3 ;
sin(π/4 - α) - √2/2sinα = sinπ/4cosα - sinαcosπ/4 - √2/2sinα = √2/2 cosα -
- √2/2 sinα - √2/2sinα = √2/2 cosα - √2sinα = √2/2 ( cosα - 2sinα );
якщо cosα = 0,5 , то √2/2 ( cosα - 2sinα ) = √2/2 ( 0,5 - 2 *0,5√3 ) =
= √2/2 ( 0,5 - √3 ) .