Решить двое играют в следующую игру: берется натуральное число, первый игрок его утраивает, второй добавляет к результату 6060, затем действия повторяются (первый утраивает результат, второй добавляет 6060 и так далее). выигравшим счиается тот игрок, который последний раз попал в отрезок [1,1000][1, 1000]. найдите наименьшее число, при старте с которого выигрывает первый игрок
Другие вопросы по теме Математика
Популярные вопросы
- Холодайка в какое время года носили...
1 - На сколько сумма дробей 11\19 и 2\19 больше их разность?...
1 - Сколько будет 169834: 31=? решить в столбик нужно...
1 - Найдите число: а)3/5 которого равны 18/25 б) 7/12 которого равны 560...
3 - Найдите наибольшее решение неравенства 9х+18 -9...
1 - Выполните смешаных чисел: 5) 7 1/2 *2 4/15 6) 5 1/6*3 1/7 7)3 3/7*2...
1 - Подводная лодка находится на глубине 300 метров. определить давление...
3 - Выпиши любое существительно и определи его морфологические признаки...
2 - Реферат на тему горные породы и минералы...
3 - 1) что образует ствол мозга? а) продолговатый и задний мосты. б) продолговатый...
3
Пусть сделано 2k-1 ходов. Тогда последним сделал ход первый. Пусть они оба начинали с числа n. Тогда на 2k-1 ходу получилось число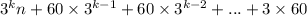 ; Упростим это выражение с формулы суммы геометрической прогрессии со знаменателем 3, имеем:
; Упростим это выражение с формулы суммы геометрической прогрессии со знаменателем 3, имеем:  ; Пусть это число оказалось равным A; То есть
; Пусть это число оказалось равным A; То есть 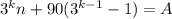 ;Общее решение этого уравнения:
;Общее решение этого уравнения: ; При этом будем стараться искать наименьшее значение n; Заметим, что знаменатель дроби в логарифме больше 90. Если результат k≥4, то числитель дроби в логарифме слишком большой. Больше 1000, а значит мы пропустили чей-то выигрыш. Тогда k=3; Результат 90+A должен быть таким, что ход второго (а это прибавление 60) выходил за интервал. То есть 90+A>1000-60+90=1030; Поскольку k=2, то 90+A=9(90+3n); Решим неравенство: 9(90+3n)>1030, откуда x>220/27, значит x≥9. Наименьшее значение n равно 9. В этом несложно убедиться. ответ: 9
; При этом будем стараться искать наименьшее значение n; Заметим, что знаменатель дроби в логарифме больше 90. Если результат k≥4, то числитель дроби в логарифме слишком большой. Больше 1000, а значит мы пропустили чей-то выигрыш. Тогда k=3; Результат 90+A должен быть таким, что ход второго (а это прибавление 60) выходил за интервал. То есть 90+A>1000-60+90=1030; Поскольку k=2, то 90+A=9(90+3n); Решим неравенство: 9(90+3n)>1030, откуда x>220/27, значит x≥9. Наименьшее значение n равно 9. В этом несложно убедиться. ответ: 9