Решить дифференциальные уравнения
подробное решение
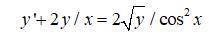
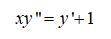
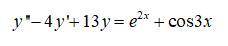
Другие вопросы по теме Математика
Популярные вопросы
- Выписать в тетрадь понятия: подсознание, познавательные процессы,память,...
1 - Составте фразы с оборото il y a из цепочек слов...
2 - 6. Складних синтаксичних цілих у текстіА. 2. Б.З. В 4. Г. 5...
3 - T-3 разделить дробной чертой на 21,всё это равно 6.Чему равен...
3 - решить задачу. Знайдіть радіуси двох кругів, які мають зовнішній...
1 - Объясните правописание орфограмм в словах: 1/ Тр..щать – 2/ предл..жить...
2 - Заходи и напишите что нибудь и получите бесплатные , и я вас...
2 - Реши неравенство (−15)(6+)≥0 Можно только ответ...
3 - Розв’яжіть задачу. Скільки грамів калій хлориду міститься в 750...
1 - 2. Жеңіс күні – бұл сан мыңдаған ұрпақ үшін ортақ мереке.Бұл...
3
1.
это уравнение Бернулли
Разделим на у в квадрате
замена:
это ЛДУ
замена:
решим отдельно:
по частям:
получаем:
общее решение
2.
делаем замену, чтобы понизить порядок:
уравнение с разделяющимися переменными
общее решение
3.
система: