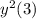Решить дифференциальное уравнение.
yy' = x, y(0)=1, (y(3))^2 = ?
Другие вопросы по теме Математика
Популярные вопросы
- Чи можна пов язати характер певних зображень із рівнем демократії?...
1 - нужно с уроком математекой 5 класс...
3 - один з кутів трикутника у 3 рази менший від другого і на 40° менший...
3 - Выполни умножение и заполни пропуски...
3 - Прямая y=6x-2 параллельна касательной к графику функции y=x²+7x-7....
2 - текст на английском. 1 Who was it for? 4 Why did you buy it? 5 Where...
3 - как средство музыкальной выразительности влияют на формирование...
2 - DF-биссектриса угла ADE, найдите все углы в △DEF (С доказательством)...
3 - Скласти рівняння реакцій C-- CO2-- CaCO3-- CaO-- Ca (OH)2-- Ca3...
3 - Как в виндоус 7 вставить копированый текст...
3
Пошаговое объяснение:
Подставим значение из условия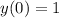
Так как корень всегда неотрицательный, ставим перед ним знак + - справа положительное число 1
Выразим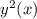
Найдем