1. Математика
  2. Решить дифференциальное

Решить дифференциальное уравнение и найти частное решение, удовлетворяющее данным условиям: (dx/(cos^2(x)*cos(+ctg(x)*sin(y)dy y=пи,при х=пи/3

34Юлия2511 34Юлия2511    1   10.07.2019 06:40    0

Ответы
Никанраа Никанраа  17.09.2020 10:51
Veamos...

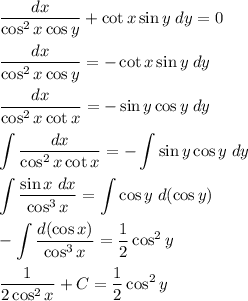
       \dfrac{dx}{\cos^2x\cos y}+\cot x\sin y\; dy=0\\ \\
\dfrac{dx}{\cos^2x\cos y}=-\cot x\sin y\; dy\\ \\
\dfrac{dx}{\cos^2x\cot x}=-\sin y\cos y\; dy\\ \\
\displaystyle
\int \dfrac{dx}{\cos^2x\cot x}=-\int \sin y\cos y\; dy\\ \\
\int \dfrac{\sin x\;dx}{\cos^3x}=\int \cos y\; d(\cos y)\\ \\
-\int \dfrac{d(\cos x)}{\cos^3x}=\dfrac{1}{2}\cos^2 y\\ \\
\dfrac{1}{2\cos ^2x}+C=\dfrac{1}{2}\cos^2 y

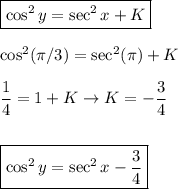
       \boxed{\cos^2 y=\sec^2x+K}\\ \\
\cos^2 (\pi /3)=\sec ^2(\pi)+K\\ \\
\dfrac{1}{4}=1+K\to K=-\dfrac{3}{4}\\ \\ \\
\boxed{\cos^2 y=\sec^2x-\dfrac{3}{4}}\\ \\

ПОКАЗАТЬ ОТВЕТЫ
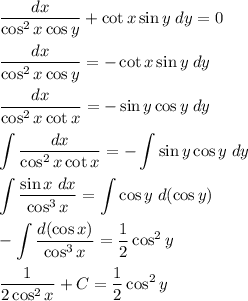
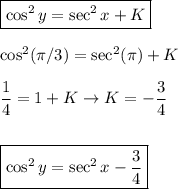
Другие вопросы по теме Математика
2006215 2006215  03.11.2020 11:08
Выпишите простые числа: 1, 9,12, 13, 51, 71, 61, 81, 91, 75, 107, 121, 728, 729, 995, 997, 1275....
Мерконюк Мерконюк  03.11.2020 11:08
351.39196:28396.66553:79644.92585:65288.32405.45​...
Yulia1421 Yulia1421  03.11.2020 11:08
Найди значение выражения.1 + (А) + (+25) + (-15) -​...
vabyn vabyn  03.11.2020 11:08
Сделайте сканворд ключевое слово геометрия...
TheFelixShow TheFelixShow  03.11.2020 11:08
Решите уравнения 1) |x| = 102) |x| = -93) 10/7 = x/34) x + ( -8) = 3...
valikkk1 valikkk1  03.11.2020 11:08
Знайти видстань миж точками A(-3;-2) B(5;-2)​...
Птичка220903 Птичка220903  03.11.2020 11:08
Числа a и b иррациональные, причём a-2b число рационально и a не равно 2b. Докажите, что число a+3 иррациональное. Рациональным или иррациональным является число...
Angelina937 Angelina937  03.11.2020 11:08
Знайти проміжок спадання функції y=(x^2-5)/(x-3)...
nelindos18 nelindos18  03.11.2020 11:08
НО 3493*. 1) Запишите четыре дроби со знаменателем 9 больше67меньше722) Запишите три дроби со знаменателем 7 больше4меньше5Но5167...
кавайнаятянка кавайнаятянка  03.11.2020 11:08
Приведите дроби 2/3 ; 7/12 ; 5/6 ; 3/16 ; 11/24 к знаменателю 48.​...

Популярные вопросы