Решить дифференциальное уравнение
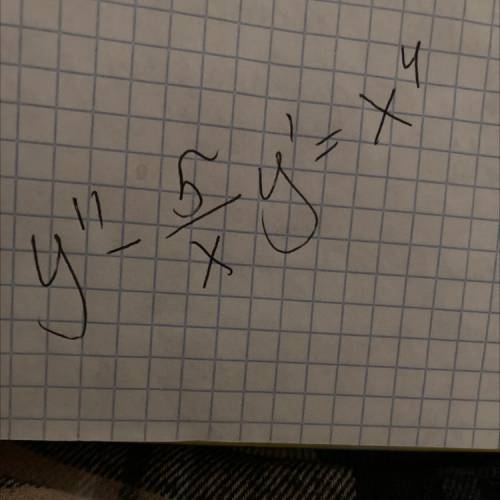
Другие вопросы по теме Математика
Популярные вопросы
- Азенкур - место сражения в 1415 году, при котором нанесли сокрушительное...
2 - Найдите лишнее слово: 1)луст; 2)фашк); 3)тиноп; 4)веерок...
2 - Составить кроссворд по полоцкому и туровскому княжеству по белоруссии...
2 - Почему многие народы принимали персидского царя как освободителя?...
3 - График функции, заданной формулой y = 3,6х +b, проходит через точку...
1 - Pomogite ! sro4no) 1) рассчитайте массу осадка, образованного при...
2 - Решить примеры (4334-4868*8)*(72405: 25) (66*541)+(59384: 13)*10...
1 - 1.какова масса тела, если на земле на это тело действует сила тяжести...
2 - Проверить предложения i don t go to school on sunday. my brother...
3 - Как найти коэффициент на графике? !...
1
Пошаговое объяснение: