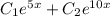Решить дифференциальное уравнение 2-го порядка. с подробным решением.
Другие вопросы по теме Математика
Популярные вопросы
- ОЧЕНЬ НУЖНО ПОДРОБНОЕ ОПИСАНИЕ. ИСПОЛЬЗОВАТЬ ФОТОМАТЧ НЕЛЬЗЯ, ТАК КАК ОН РЕШАЕТ...
3 - Is tne toy soldier in tne toy box? Нужно ответить на этот вопрос по английски...
3 - 1. This is a winter sport. This is a team sport. This is an outdoor sport. Two...
3 - В чём заключалась налоговая реформа проводимая надир шахом...
2 - Соединить предложение с правильным ответом. Один ответ лишний его использовать...
1 - Какое сможете из 18,19,20 номеров, напишите...
3 - Решите уравнение под а и задание под б. Можно мне решение, надо разобраться...
3 - Письмо будущему поколению о афганской войне...
1 - найди первый член арифметической прогрессии, разность которой равна -4, а сумма...
1 - Постройте график и опишите свойства функции (14.13—14.17): 14.14.1) f(x) = 2x²...
1
y=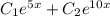
Пошаговое объяснение:
y"-15y'+50y=0
Замена
y"=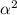 y'=
y'=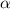 y=
y=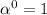
y=