решить дифференциальное уравнение
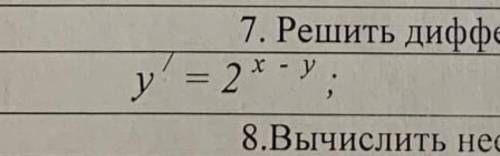
Другие вопросы по теме Математика
Популярные вопросы
- Переводите предложения в пассивном залоге. ВОТ эти предложение •A porous...
2 - Қай планетада жер сияқты төрт мезгіл бар...
1 - Определите жанры песеного искусства Казахстана в XIX в НАДО...
2 - Choose the right answer: 1. Fruit and vegetables help our eyes, skin andA)earsB)hair...
2 - Під час гібридної війни які загрози небезпечніші — внутрішнє протистояння...
2 - 3.Расположите по порядку оформление реферата. (укажите цифрами в первом столбце)ЗаключениеВведениеТитульная...
3 - СОР. Неравенство (x-a)(4x-2)(x+b) 0 имеет решение (-4;0.5)(5;+бесконечности)....
2 - Винесіть спільний множник за дужки:6x(a - 2) + 8y(а - 2) + 4c(2-а) повний...
3 - Определите верные или неверные утверждения. №УтвержденияВерно/неверно1В конце...
3 - Перечислите этапы решения задачи с компьютера. выбери правильные ответы из...
1
общее решение