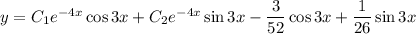Решить дифф.уравнения-y'' + 8 y'+25y=2sin 3x
Другие вопросы по теме Математика
Популярные вопросы
- Жиынтық күн радиациясының шамасы неге байланысты....
2 - Задание № 1. Объясни, как возникли племена каракитаев, используя...
3 - Подготовьте тезисный план, обьеденив сообщения учиников....
3 - При исследовании пробы вещества массой m было установлено, что...
2 - ЖАУАПТАРЫ БАРМА БОЛСА БЕРИНДЕРШ ГЕОМЕТРИЯ 8 СЫНЫП ...
3 - Я СЕЙЧАС ВЫРЕЖУСЬ ответ желательно в паинте или что-то вроде,...
3 - | What is situated in the middle of TrafalgarSquare?A monument...
1 - Обсудите вопросы, предложенные в учебнике, разделив их на тонкие...
1 - Напишите на листочке и сфоткайте...
3 - Абайдың ақындығын танытатын көркемдегіш құралдарын тауыполардың...
2
Имеем линейное неоднородное дифференциальное уравнение (ЛНДУ) с постоянными коэффициентами.
Общее решение этого уравнения: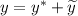
Воспользуемся методом Эйлера. Подстановка: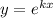 .
.
Тогда получим характеристическое уравнение:
Имеем комплексно-сопряженные корни вида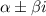
Здесь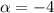 и
и 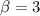
Тогда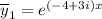 и
и 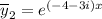
Используем формулу Эйлера: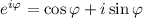
Значит,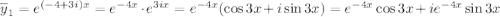
Таким образом, фундаментальная система решений: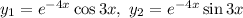 — линейно независимые функции.
— линейно независимые функции.
Общее решение: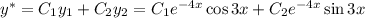
Правая часть второго типа: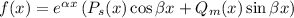
В нашем уравнении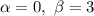 и не совпадает корнем однородного ЛДУ, а именно:
и не совпадает корнем однородного ЛДУ, а именно: 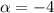 и
и 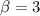 , поэтому
, поэтому 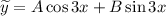 , где
, где 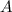 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Здесь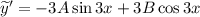 и
и 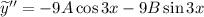
Подставим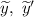 и
и 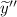 в заданное уравнение со специальной правой частью:
в заданное уравнение со специальной правой частью:
Частное решение: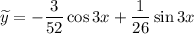
Общее решение заданного дифференциального уравнения:
ответ: