решить. Дано: ▲MNO и ▲QPO
MO=OQ ; NO = PO
Доказать: MN = PQ
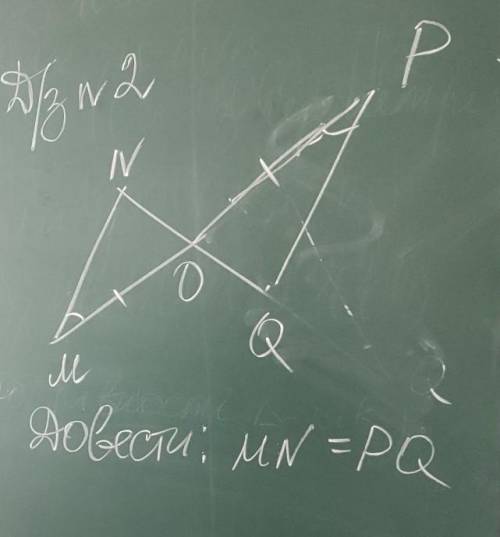
Другие вопросы по теме Математика
Популярные вопросы
- Дайте морфологический разбор слова: (по) цели...
3 - Как сделать орфографический разбор слов: идёшь, услышешь (как написать)...
1 - Любые 3 предложения матрешки и 3 гуси...
2 - Счего можно начать писать сочинение на тему национальные праздники узбекистана...
1 - Какие цифры можно поставить вместо*в число 5*4, чтобы оно было кратно 3, но не...
1 - Начерти 2 отрезка так, чтобы один из них был короче другого на 3 см, а они составляли...
3 - Гоночный автомобиль за 10 мин проезжает путь равный 50 км. определите его среднюю...
2 - 20 надо прям найдите число обратное1) разности чисел 8 3/4 и 7 5 /16 2) произведению...
1 - Есть ли приставка у слов произощло уничтожает спускались...
3 - Решите уравнение ,используя логарифмы log7^x+log7^38=log7^19+log7^3( )...
3
Исходя из данных, у нас есть два равенства: MO=OQ и NO=PO. Мы хотим доказать, что MN=PQ.
Для начала, построим отрезки MP и NP, чтобы получить еще два треугольника: △MNP и △POQ.
Теперь мы можем применить свойство равенства треугольников, которое гласит, что если у двух треугольников равны длины двух сторон и угол между ними, то треугольники равны.
У нас уже есть равенство MO=OQ.
Также, благодаря свойству треугольников, мы можем сказать, что NM=QP, так как это стороны треугольников △MNO и △QPO, и у них с одной стороны равны длины.
Теперь мы должны показать, что треугольники △MNP и △POQ равны. Для этого мы должны доказать, что у них равны две стороны и угол между ними.
У нас уже есть равенство NO=PO.
Мы также можем сказать, что угол NMP = QPN (угол между сторонами NM и QP), так как это вертикальные углы и по определению вертикальных углов они равны.
Таким образом, мы доказали, что у треугольников △MNP и △POQ равны две стороны и угол между ними, следовательно, эти треугольники равны.
А значит, MN=PQ, т.к. это сторона треугольников △MNP и △POQ, которые являются равными.
Следовательно, доказано, что MN = PQ.