Решить данные примеры: 1) найти производную функции ![f(x)=\frac{1}{\sqrt[2]{x^{3} } }](/tex.php?f=f(x)=\frac{1}{\sqrt[2]{x^{3} } }) 2) взять определённый интеграл
2) взять определённый интеграл ![\int\limits^1_0 3{\sqrt[3]{x^{2} } } \, dx](/tex.php?f=\int\limits^1_0 3{\sqrt[3]{x^{2} } } \, dx) 3) найти производную сложной функции
3) найти производную сложной функции 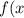=e^{-7x+2x})
Другие вопросы по теме Математика
Популярные вопросы
- Make true sentences.There is a opposite my school...
3 - В левом колене сосудов - U вода высотой 40 см, в правом колене...
3 - Не стомилась козацька сила за повистю Тарас бульба...
2 - Письменно проанализировать ключевой эпизод (по своему мнению)...
3 - Қалидың күлімсірегенінен Манаптың тұла бойы неге дір ете қалды?...
3 - написать сочинение по теме: 1)Деградация человеческого материала...
3 - 245. Напишите: а) все правильные дроби со знаменателем 9;6) все...
2 - решить вычислите площадь боковой поверхности правильной усечённой...
3 - 1. Как объединены между собой простые предложения в составе сложного...
1 - А) 1,84 : 0,8 = ??Б)181,3 : 7,4 = ?? В СТОЛБИК !В)86,1 : 0,42...
1
Пошаговое объяснение:
вот
1. f'(x)=(1/√x³)'=(x^(-3/2))'=-1.5*x⁻⁵/²=-3/(2x²√x)
2. Сначала неопределенный интеграл,
∫3*(x^(2/3))dx=(3*x²/³⁺¹)/(2/3+1)=(9*x⁵/³)/5; теперь по формуле Ньютона -Лейбница возьмем определенный интеграл, подставив нижний и верхний пределы интегрирования. В нижнем ноль, в верхнем 9/5
Значит, 9/5-0=1.8
3. f'(x)=(e⁻⁷ˣ⁺²ˣ)'=(e⁻⁵ˣ)'=-5*e⁻⁵ˣ