решить №55 и №56, с подробным объяснением (словами)
Другие вопросы по теме Математика
Популярные вопросы
- Разбери предложение.весной в саду цветёт душистый ландыш....
3 - Длина улицы 600 м, а ширина 12 м. улицу покрыли асфальта. на каждые 100 м требуется...
3 - Дана линейная функция y= -3,9x.найдите х,если y=0.y=-3,9.y=78....
3 - Составьте пару предложений о екатерине 2 (заранее)...
3 - 1.пасленовые растения широко используються в пищу.например у бклажана-плоды,у картофеля...
2 - Решите уравнение 8 (х - 1,4) = 0,56...
3 - Твір на тему чи можна пробачити ворогові...
1 - Все свои только сделайте умоляю вас составить сочинение кем ты хочешь стать(программистом...
3 - Решить уравнение: z^2+16z+60=0 найдите два корня...
1 - Что можно написать по теме рассказ о благотворительности...
3
55) Пользуемся свойствами: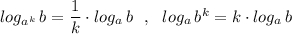 .
.
56) Решаем аналогично.