Разверткой боковой поверхности цилиндра является прямоугольник, у которого одна из сторон вдвое больше другу.бична поверхность цилиндра

Question

Математика: Разверткой боковой поверхности цилиндра является прямоугольник, у которого одна из сторон вдвое больше другу.бична поверхность цилиндра 20см2.определить его полную поверхность

Kg1 · Answer

Обозначим одну из сторон прямоугольника развертки боковой поверхности через a, тогда вторая будет 2a

$S=2a*a=2a^{2} =20$

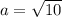
Откуда $a=\sqrt{10}$

Одна из сторон этого прямоугольника одновременно равна длине окружности основания цилиндра. Если обозначим радиус основания цилиндра через R, то можем записать:

$2\pi R=\sqrt{10} \\R=\frac{\sqrt{10} }{2\pi }$