1. Математика
  2. разобраться как такие лимиты

разобраться как такие лимиты нахоить Понимаю, что нужно перевести на экспоненту но не знаю что дальше


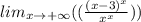
lim_{x \to +\infty} ((\frac{(x-3)^x}{x^x}))

натаха37 натаха37    2   30.06.2021 04:04    0

Ответы
yulyaakimova0 yulyaakimova0  30.07.2021 04:42

Пошаговое объяснение:

\displaystyle \lim_{x \to \infty} \frac{(x-3)^x}{x^x}

сначала сделаем преобразования

\displaystyle \frac{(x-3)^x}{x^x}=x^{-x}*(x-3)^x=e^\displaystyle{xln(x-3)-xlnx

тогда

\displaystyle \lim_{x \to \infty} e^\displaystyle{xln(x-3)-xlnx}}=}e^{\displaystyle \lim_{x \to \infty} (xln(x-3)-xln)}

теперь ищем предел

{\displaystyle \lim_{x \to \infty} (xln(x-3)-xlnx})

преобразуем

\displaystyle xln(x-3)-xlnx}= x(ln(x-3)-lnx) =\frac{ln(x-3)-lnx}{1/x}

теперь применим правило Лопиталя

\displaystyle \lim_{x \to \infty} \frac{ln(x-3)-lnx}{1/x} = \lim_{x \to \infty} \frac{(ln(x-3)-lnx)'}{(1/x)'} = \lim_{x \to \infty} a_n \frac{\frac{1}{x-3} -\frac{1}{x} }{-\frac{1}{x^2} } =

\displaystyle \lim_{x \to \infty}- \frac{3x}{x-3} =-3 \lim_{x \to \infty} \frac{x}{x-3} =-3

тогда получим

\displaystyle e^{\displaystyle \lim_{x \to \infty} (xln(x-3)-xln)}=e^{-3}

и вот ответ

\displaystyle \lim_{x \to \infty}\frac{(x-3)^x}{x^x} =e^{-3}=\frac{1}{e^3}

ПОКАЗАТЬ ОТВЕТЫ
lambert1337 lambert1337  30.07.2021 04:42

e^{-3}

Пошаговое объяснение:\lim\limits_{x\to+\infty}\dfrac{(x-3)^x}{x^x}=\lim\limits_{x\to+\infty}\left(\dfrac{x-3}{x}\right)^x=\lim\limits_{x\to+\infty}\left(1-\dfrac{3}{x}\right)^x=\lim\limits_{x\to+\infty}\left(1-\dfrac{3}{x}\right)^{\left(-\dfrac{x}{3}\right)\cdot {(-3)}}=\lim\limits_{x\to+\infty}\left(\left(1-\dfrac{3}{x}\right)^{-\dfrac{x}{3}}\right)^{-3}=\left[-\dfrac{x}{3}=t\right]=\lim\limits_{t\to-\infty}\left(\left(1+\dfrac{1}{t}\right)^{t}\right)^{-3}=(*)Используем второй замечательный предел \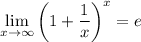lim\limits_{x\to\infty} \left(1+\dfrac{1}{x}\right)^x=e и непрерывность функции f(x)=x^{-3}:

(*)=\left(\lim\limits_{t\to-\infty}\left(1+\dfrac{1}{t}\right)^{t}\right)^{-3}=e^{-3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Foksit2006 Foksit2006  19.05.2019 07:30
Расскажи о весне по плану 1.погода 2.деревья и цветы весной 3.животные весной 4.туд взрослых и детей...
ArtemkaRus71 ArtemkaRus71  19.05.2019 07:30
Дополни условие числом и реши её.высота кирпичного м, а деревянного 9 м. на сколько метров кирпичный дом выше,чем деревянный?...
LinaCat123456789 LinaCat123456789  19.05.2019 07:30
5/9 школьного отряда были девочки, остальная часть были мальчики, которых было на 4 человека меньше, чем девочек. сколько девочек и мальчиков было в отряде?...
Алиса623 Алиса623  19.05.2019 07:30
Ваквариуме морского музея 444 моллюска. из них гребешков в 5 раз больше ,чем мидий ,а жемчужниц столько сколько ,сколько мидий и гребешков вместе. определите число моллюсков...
Asyu666 Asyu666  19.05.2019 07:30
Всеобщая связь - основной принцип существования мира.докажите его справедливость на примере взаимодействия систем : человек - земля,, земля - космос,, человек -...
lizza3429 lizza3429  19.05.2019 07:30
Риторика. нужно придумать шуточный рецепт на темы: сластены в миранде или щи из кислых детей. (один по выбору) заранее большое...
nekit3221 nekit3221  19.05.2019 07:30
Мальчик друзьям сказал что вчера ему было 10 лет а наследующий день ему исполнилось 13 ! !...
avisotska avisotska  19.05.2019 07:30
Составить кроссворд на тему: термины. 10 слов...
Yabloco4 Yabloco4  19.05.2019 07:30
Впервый день туристы км, во второй день они пути, пройденого в первый и 5/7 того пути, что в третий день. какую часть всего пути туристы в первый день?...
Віка12341 Віка12341  19.05.2019 07:30
А) на доске 25×25 расставлены 99 шашек, причём их расположение симметрично относительно одной из диагоналей доски. докажите, что одна из шашек стоит на этой диагонали. б) пусть...

Популярные вопросы