Разложить многочлен на линейные множители, если известен один корень z0.
( 10 номер)
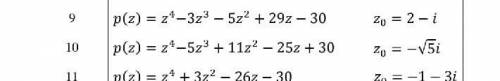
Другие вопросы по теме Математика
Популярные вопросы
- Знайдіть запозичені слова та поясніть правопис м якого знака в...
2 - 1.гиппократ учил, что врач должен лечить не болезни, а больного,принимал...
1 - Sin8a×cos12a х-умножения a-альфа...
1 - Распишите хлоропохідне насиченого вуглеводню має відносну масу...
2 - Охарактеризуйте взаємовідносини між сеньйорами і васалами...
3 - Деление с остатком 65.306/121 66.500/3.200...
2 - A) в урні є 9 червоних і 10 синіх куль. знайдіть ймовірність того,...
2 - Составьте и запишите пять предложений. тема мини-текста времена...
3 - 1-1 скоко будет скажиме мне всего 4 100...
1 - Доберіть по 2 пари електролітів, які реагуютьу розчині з утворенням:...
2
Если известен один комплексный корень многочлена z_0=2+3i , то известен и второй корень, сопряжённый ему, это будет z_1=2-3i . Значит в разложении на линейные множители многочлена p(z) будут присутствовать такие множители :
(z-(2+3i))\cdot (z-(2-3i))=(z-2-3i)\cdot (z-2+3i)=z^2-4z+13
Разделим многочлен p(z) на многочлен z^2-4z+13 . Получим
\frac{z^4-9z^3+39z^2-89z+78}{z^2-4z+13}=z^2-5z+6z^2-5z+6=0\; \; \to \; \; z_2=2\; ,\; z_3=3\; \; (teorema\; Vieta)\; \; \Rightarrow z^2-5z+6=(z-2)(z-3)
Окончательно получим
z^4-9z^3+39z^2-89z+78=(z-2-3i)(z-2+3i)(z-2)(z-3)
Пошаговое объяснение: