Расстояние между двумя пристанями равно 162 км. Из них одновременно навстречу друг другу вышли две лодки, скорости которых в стоячей воде равны. Через 3 ч. лодки встретились. Скорость течения реки равна 2 км/ч. Скорость лодки в стоячей воде равна
км/ч.

Сколько километров до места встречи пройдёт лодка, плывущая по течению?
км.
Сколько километров до места встречи пройдёт лодка, плывущая против течения?
км.

1) 162 : 3 =54 км/ч - скорость сближения

2) 54:2=27 км/ч - скорость каждой лодки в стоячей воде

3) 27 -2=25 км/ч - скорость против течения

4) 27+2=29 км/ч - скорость по течению

5) 25*3=75 км - пройдёт лодка , плывущая против течения

6) 29*3=87 км - пройдёт лодка , плывущая по течению

v относительная=v за течением+ v против течения=(v+2)+(v-2)=2v

l =v относительная*t = 2v * t ⇒2v=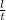=54 км/ч⇒v=54 км/ч :2 =27 км/ч

v по течению=27 км/ч+2км/ч=29км/ч

v против течения=27 км/ч-2км/ч=25км/ч

l по течению=t*v течению= 87 км

l против точения=t*v против течения= 75 км

ответ: 87 км, 75 км.

P.S. я мог сделать ошибки в словах, потому что я не русский.