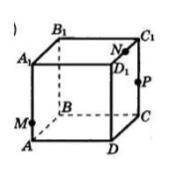
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 построить сечение проходящее через точки M, N, P (С объяснениями)

Для построения сечения, проходящего через точки M, N и P, необходимо использовать плоскость, которая будет проходить через эти точки.

Шаг 1: Найдем плоскость, проходящую через точки M, N и P.
Для этого выберем два вектора соединяющих данные точки. Пусть вектор A1M будет равен AM, вектор CP будет равен CB - CA и вектор B1N равен NB - AN.

А1M = AM = A1M1 + M1M
CP = CB - CA = C1B1 - C1A1 + AA1 + AB
B1N = NB - AN = NB1 + B1N1 + A1N = N1B1 + B1N1 + NN1 + AN

Шаг 2: Построим плоскость.

Для построения нам понадобится найти нормаль к этой плоскости.

Воспользуемся свойством векторного произведения, согласно которому векторное произведение двух векторов равно вектору, перпендикулярному плоскости, образованной этими векторами. Векторное произведение записывается как:

N = AB x AC, где AB и AC - выбранные векторы.

Таким образом, вектор нормали N будет равен векторному произведению:

N = AB x AC

Шаг 3: Используя полученный вектор нормали N и одну из точек, например, точку M, можно записать уравнение плоскости Ax + By + Cz + D = 0, где (x, y, z) - координаты точки, A, B, C - компоненты вектора нормали N, D - получаемый коэффициент.

Так как для точки M вектор нормали будет перпендикулярен к плоскости, то мы можем записать уравнение вида:

A(x - x1) + B(y - y1) + C(z - z1) = 0, где (x1, y1, z1) - координаты точки M.

Шаг 4: Подставим в уравнение координаты точек N и P и найдем значения A, B и C.

A(x - x1) + B(y - y1) + C(z - z1) = 0
A(x - x2) + B(y - y2) + C(z - z2) = 0

Шаг 5: Определим координаты точек M, N, P и заменим их в уравнение плоскости, чтобы получить конкретное уравнение.

Шаг 6: Используя полученные коэффициенты A, B и C, а также конкретное уравнение плоскости, можно построить сечение параллелепипеда, проходящее через точки M, N и P.

Для этого проведем плоскость с использованием полученной плоскости и найденных координат точек. Полученное сечение будет пересекать стороны параллелепипеда ABCDA1B1C1D1 в точках, проекции которых соответствует точкам M, N и P.