Радиус окружности, описанной около треугольника, равна 11 корней из 3. найдите сторону треугольника

Question

Математика: Радиус окружности, описанной около треугольника, равна 11 корней из 3. найдите сторону треугольника

dartwaoder20hdhxgs · Answer

Условие неполное. Добавлю в условии, что треугольник правильный.

Задача. Радиус окружности, описанной около правильного треугольника, равна 11 корней из 3. Найдите сторону треугольника.

Можно найти сторону треугольника через готовые формулы, но покажу как это можно доказать формулу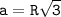 $\tt a=R\sqrt{3}$

Обозначим стороны треугольника AC = BC = AB = a(стороны у прав. треугольника равны ведь).

Применим обобщенную теорему синусов: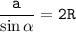 $\tt \dfrac{a}{\sin \alpha} =2R$

У правильного треугольника все углы по 60°, следовательно

$\tt \dfrac{a}{ \sin60^{\circ}} =2R~~~\Rightarrow~~~\dfrac{a}{\cfrac{\sqrt{3}}{2}} =2R ~~\Rightarrow~~~ \boxed{\tt a=R\sqrt{3}}$

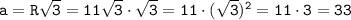
Получим: $\tt a=R\sqrt{3}=11\sqrt{3} \cdot \sqrt{3} =11\cdot(\sqrt{3} )^2=11\cdot 3=33$

ответ: 33.