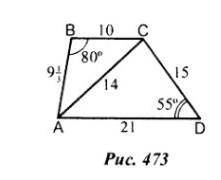
Р. 473 ав= 9,1/3 Lв= 80°,ас=14, ад=21,Lд=55°, сд=15,вс=10 найти Lвса
Другие вопросы по теме Математика
Популярные вопросы
- Очень короткое содержание Редьярд Киплинга про Восток и Запад...
2 - Выпишите предложения с прямой речью знаки препинания не расставлены,...
2 - Написать очень кратко о всех 13 подвигов Геракла по книге...
1 - Н а некрасов мороз красный нос что понравилось...
1 - Две бригады, работая вместе, вспахали поле за 4 часа. За сколько...
2 - интересует только чертеж )...
3 - Впишите соответствующее выражение...
3 - визначте маси целюлози та нітратної кислоти, які потрібно витратити...
1 - Помагите пажадуйса нужо составить 5 упражнений на премере этого...
3 - Повнолітні діти скорочено...
2
Теорема косинусов утверждает, что для треугольника ABC с сторонами a, b и c, и углом α напротив стороны a, углом β напротив стороны b и углом γ напротив стороны c, справедливо следующее равенство:
c^2 = a^2 + b^2 - 2abcos(γ)
В данном случае, мы можем применить эту теорему к треугольнику ВСА.
Из условия дано следующее:
ав = 9,1/3
Lв = 80°
ас = 14
ад = 21
Lд = 55°
сд = 15
вс = 10
Мы хотим найти значение Lвса.
Для начала, давайте найдем значение стороны ВС, используя формулу косинусов:
вс^2 = ас^2 + сд^2 - 2ас⋅сд⋅cos(Lд)
вс^2 = 14^2 + 15^2 - 2⋅14⋅15⋅cos(55°)
вс^2 = 196 + 225 - 2⋅14⋅15⋅0,573576436351
вс^2 = 196 + 225 - 20⋅0,573576436351
вс^2 = 196 + 225 - 11,47152613081
вс^2 = 420,5284738692
вс ≈ √420,5284738692
вс ≈ 20,51
Теперь у нас есть значение стороны ВС, а также значение стороны АВ, которое равно 9,1/3. Чтобы найти Lвса, мы можем использовать формулу синусов:
sin(Lвса) = (ав⋅sin(Lд)) / вс
sin(Lвса) = (9,1/3⋅sin(55°)) / 20,51
sin(Lвса) = (9,1/3⋅0,819152044289) / 20,51
sin(Lвса) = 0,75076551282 / 20,51
sin(Lвса) ≈ 0,036625324897
Теперь мы можем найти значение Lвса, используя обратную функцию синуса (асинус):
Lвса = asin(0,036625324897)
Lвса ≈ 2,11°
Таким образом, значение Lвса примерно равно 2,11°.