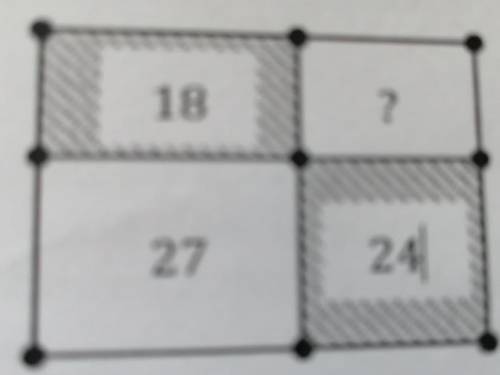
ПРямоугольный лист двумя пересекающимися линиями разделили на 4 прямоугольника. Площади двух противоположных частей равны 18 см² и 24 см²(показано на рисунке). Площадь третьей части равен 27 см². Чему равна площадь четвёртой части?

Чтобы решить задачу, мы можем использовать знания о площади прямоугольника и о свойствах пересекающихся линий.

Обозначим прямоугольник, на котором была проведена разделительная линия, как ABCD. Всего на рисунке показаны 4 прямоугольника: ABFE, ECGF, GCHD и DHAB.

У нас уже даны площади двух противоположных прямоугольников: ABFE и GCHD, которые равны 18 см² и 24 см² соответственно. Обозначим эти площади как S1 и S2.

Также нам дана площадь третьего прямоугольника, ECGF, равная 27 см². Обозначим эту площадь как S3.

Мы знаем, что общая площадь прямоугольника ABCD равна сумме площадей всех 4 прямоугольников. Обозначим общую площадь как S, а площадь четвертого прямоугольника как S4.

Таким образом, у нас имеется следующее уравнение:
S = S1 + S2 + S3 + S4.

Мы должны найти значение S4.

Мы также знаем, что S1, S2 и S3 равны 18 см², 24 см² и 27 см² соответственно. Подставим эти значения в уравнение:

S = 18 + 24 + 27 + S4.

Найдем сумму чисел 18, 24 и 27 для получения общей площади:

S = 69 + S4.

Теперь мы можем найти значение S4, выделив его в уравнении:

S4 = S - 69.

Но мы не знаем общую площадь S прямоугольника ABCD.

Для нахождения S, мы можем использовать свойство пересекающихся линий. Когда пересекающиеся линии делят прямоугольник на 4 прямоугольника, площадь четырех прямоугольников равна произведению длин и ширины четырех прямоугольников.

Поэтому S = длина * ширина.

Давайте обозначим длину прямоугольника как L и ширину как W.

Тогда S = L * W.

Теперь мы можем привести наше уравнение к виду, чтобы оно зависело только от L и W:

S4 = L * W - 69.

Однако нам все равно не даны значения длины и ширины прямоугольника. Поэтому нам нужно использовать другую информацию, которую нам дали.

На рисунке мы видим, что одна из сторон разделительной линии проходит через произвольную точку F, которая находится на прямой BC. Это означает, что точка F разделяет сторону BC на две равные части.

Это говорит нам о том, что L/2 = 24, где L/2 - половина длины прямоугольника, соответствующая S2.

Отсюда мы можем найти значение L:

L/2 = 24,
L = 24 * 2,
L = 48.

Теперь у нас есть значение длины прямоугольника.

Чтобы найти значение ширины прямоугольника, мы можем использовать информацию о площади одного из противоположных прямоугольников.

Например, площадь прямоугольника ABFE равна 18 см². Обозначим его длину как L1 и ширину как W1.

Тогда S1 = L1 * W1 = 18.

Мы знаем, что L1 = L - L/2 = 48 - 24 = 24, где L - длина прямоугольника и L/2 - половина длины прямоугольника, соответствующая S2.

Подставим такое значение L1 в уравнение:

18 = 24 * W1,
W1 = 18 / 24,
W1 = 0.75.

Теперь у нас есть значение ширины прямоугольника.

С помощью полученных значений L и W мы можем вычислить общую площадь S:

S = L * W = 48 * 0.75 = 36.

И, наконец, мы можем найти значение S4, подставив значение S в наше предварительное уравнение:

S4 = S - 69 = 36 - 69 = -33.

Ответ: площадь четвертой части равна -33 см².

Однако отрицательное значение площади не имеет физического смысла в данной задаче. Вероятно, в задаче есть ошибка или противоречие. В таком случае, следует проверить условие задачи и исключить возможные ошибки в постановке.