1. Математика
  2. Прямая 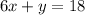пересекает гиперболу

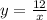Прямая 6x+y=18 пересекает гиперболу y=\frac{12}{x} в точках А и В. Найти длину отрезка АВ. Варианты ответов:
1) 12;
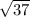2) \sqrt{37};
3) 42;
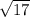4) \sqrt{17};
5) 24

lukianova201720 lukianova201720    1   15.07.2021 14:00    2

Ответы
aregv aregv  14.08.2021 14:45

Здравствуйте!

\sqrt{37}

Пошаговое объяснение:

Для начала стоит найти точки А и В. Чтобы сделать это, надо решить систему уравнений:

\displaystyle\left \{ {{6x+y=18} \atop {y=\frac{12}{x}}} \right. \\\\\left \{ {{6x+\frac{12}{x}=18} \atop {y=\frac{12}{x}}} \right. \\\\6x+\frac{12}{x} =18\\\frac{6x^{2} +12}{x} =18\\\\6x^{2} +12=18x\\x^{2} +2=3x\\x^{2} -3x+2=0\\x_{1} =1 \:\:\:\:u \:\:\:\:x_{2}=2\\\left \{ {{x_{1}=1} \atop {y_{1}=\frac{12}{1}}} \right.\left \{ {{x_{1}=1} \atop {y_{1}=12}} \right.\\\left \{ {{x_{2}=2} \atop {y_{2}=\frac{12}{2}}} \right.\left \{ {{x_{2}=2} \atop {y_{2}=6}} \right.

Получаем точки А(1; 12) и B (2; 6).

Чтобы найти длину отрезка, пользуемся формулой:

\displaystyle\sqrt{(x_{2}-x_{1} )^{2} +(y_{2}-y_{1} )^{2} }

Подставляем значения:

\displaystyle\sqrt{(x_{2}-x_{1} )^{2} +(y_{2}-y_{1} )^{2} } =\\=\sqrt{(2-1 )^{2} +(12-6 )^{2} } =\sqrt{1+6^{2} } =\sqrt{37}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Dmutrenkovladuslav12 Dmutrenkovladuslav12  01.11.2020 21:17
Отметьте на числовой прямой все целые значения х, при которых будет верным неравенство: |x| 3,6....
Yaroslavdonskk Yaroslavdonskk  01.11.2020 21:17
. Мына епилярын стандарт түрінде жазылған нұсқасын таңдаңыз 200 000; 150 000,23000A) 210:1,510 2.310 6) 210:1,5102.310B) 210:1,510 2.310 C) 210*;1.5102.310...
Надюфка1997 Надюфка1997  01.11.2020 21:17
Исследовать ряд на абсолютную и условную сходимость ∞∑ n=1 (-1)^n(n+3)/n...
Б45 Б45  01.11.2020 21:16
Агрофірма має 140 га землі, 16% якої займає яблуневий сад. Знайдіть площу саду....
malia1011 malia1011  01.11.2020 21:16
Математика 23-беттеги 6 есеп​...
ЭймиКаннет ЭймиКаннет  01.11.2020 21:15
Тжб математика көмектесіңші​...
Лолита171107 Лолита171107  01.11.2020 21:15
Спростіть вираз y+3/2y+2-y+1/2y-2+3/y^2-1...
superyarmola201 superyarmola201  01.11.2020 21:15
В какой горизонтальной четверти расположены углы: 1) tg 12 градусов, 137 градусов, 189 градусов, 280 градусов. 2) ctg 68 градусов, 163 градуса, 237 градусов, 342...
Neznat13 Neznat13  30.08.2019 07:50
Условия бочке было 200 литров бензина когда из него отлили несколько литров бензина то в ней осталось уже в 4 раза больше бензина чем отлили сколько литров бензина...
Tanya5463 Tanya5463  30.08.2019 07:50
Как решить уравнение (502-2)x a=1000...

Популярные вопросы