прямая 5x-12y+4=0 касательная к окружности с центром в точке (2;-1). Составьте уравнение этой окружности.

Ответы

vikabosch 14.03.2021 22:00

$(x-2)^2+(y+1)^2= \frac{676}{5}$

Пошаговое объяснение:

Уравнение окружности с центром в точке (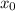 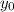$x_{0}$ , $y_{0}$ ) радиуса r выглядит так:

$(x-x_{0})^2+(y-y_{0})^2 = r^2$ .

Радиус в анном случае ищется как расстояние от точки до прямой(касательной)

$r = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2} }$

Подставляем известную точку в уравнение окружности и записываем ответ

$(x-2)^2+(y+1)^2= (\frac{26}{\sqrt{4+1}})^2$

ПОКАЗАТЬ ОТВЕТЫ

Timpo 19.01.2024 21:42

Добрый день! Давайте решим эту задачу пошагово.

У нас есть данный уравнение прямой: 5x - 12y + 4 = 0 и центр окружности (2;-1). Мы должны найти уравнение окружности, касательной к этой прямой.

1. Чтобы прямая была касательной к окружности, расстояние от центра окружности до прямой должно быть равно радиусу окружности.

2. Радиус окружности можно найти по формуле: r = √((x - a)² + (y - b)²), где (a; b) - координаты центра окружности, а (x; y) - координаты любой точки на окружности.

3. Подставим координаты центра окружности в формулу: r = √((x - 2)² + (y - (-1))²), которая упрощается до r = √((x - 2)² + (y + 1)²).

4. Теперь нужно найти расстояние от прямой до центра окружности при помощи формулы: d = |Ax + By + C| / √(A² + B²), где A, B и C - коэффициенты уравнения прямой 5x - 12y + 4 = 0.

5. Подставим значения коэффициентов A, B и C в формулу: d = |5*2 + (-12)*(-1) + 4| / √((5)² + (-12)²), после упрощения получим d = |10 + 12 + 4| / √(25 + 144), что равносильно d = |26| / √169.

6. Расстояние d равно радиусу окружности r: |26| / √169 = r.

7. Преобразуем уравнение, чтобы избавиться от знака модуля: 26 / √169 = r.

8. Упростим: 26 / 13 = r.

Таким образом, уравнение окружности с центром в точке (2;-1) и радиусом r = 2 имеет вид: (x - 2)² + (y + 1)² = 4.

Надеюсь, это решение понятно и полезно для вас. Если у вас есть еще вопросы, не стесняйтесь задавать!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика