Провести полное исследование функции:
y = 1 / x * lnx
Другие вопросы по теме Математика
Популярные вопросы
- Что ты сделаешь, чтобы остановить кровь из раны? А) смажу рану йодом...
1 - Какие проблемы для человека в хозяйственной деятельности создают снежные...
3 - Артериальное кровотечение возникает: А) при поверхностном ранении в случае...
1 - Самым надежным остановки кровотечения в случае повреждения крупных артериальных...
3 - Назовите факторы выживания человека в природных условиях. А) объективные;...
3 - Какие территории наиболее подвержены лавинной опасности в нашей стране?...
1 - Что необходимо предпринимать человеку, оказавшемуся в чрезвычайной ситуации...
2 - Основными поражающими факторами оползней, селей, обвалов и снежных лавин...
2 - Назовите основные причины страха? А) испуг; б) утрата контроля за своим...
3 - Основной причиной крупных обвалов является: а)таяние ледников; б)землетрясения;...
3
разрыв второго рода
6. Асимптотывертикальные:
горизонтальные:
расставим знаки второй производной:
- 0 - 1 +
----------------------------|-------------------------------|---------------------
(не определена) (выпуклая вверх) (выпуклая вниз)
Точек перегиба нет, при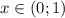 выпуклая вверх, при
выпуклая вверх, при 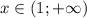 выпуклая вниз
выпуклая вниз
10. Четность - нечетностьобщего вида
11. График