Проверьте являются ли булевы функции f1 и f2 эквивалентными. Под буквой Б
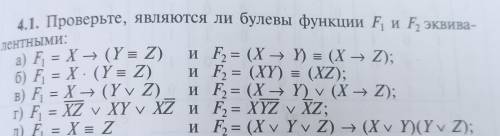
Другие вопросы по теме Математика
Популярные вопросы
- Сурет ушбұрыш, шенбер, төртбурыш сиякты геометриялык пішіндер аркылы...
1 - Вот текст 1)Anna is sitting on the sofa and she s sending Lucy an...
3 - Какое произведение начинается данным двустишием?...
1 - Нужно Два стрелка произвели по одному выстрелу. Вероятность попадания...
3 - приведите правильно построенные чертежи, если на кординатной прямой...
3 - Прочитай текст определи стиль текста, подтверди 2 аргументами Многие...
2 - Complete the sentences with at, in, or on. Example: We got married...
1 - 1) разложить многочлен на множители методом вынесения за скобку а)...
1 - Выберите верный ответ. Выберите один ответ: a. если х∈А ∩ В, то х...
2 - Які на вашу думку могли скластися відносини між різними верствами...
1
Давайте начнем с построения таблицы истинности для функций f1 и f2.
| A | B | C | f1 | f2 |
|---|---|---|----|----|
| 0 | 0 | 0 | ? | ? |
| 0 | 0 | 1 | ? | ? |
| 0 | 1 | 0 | ? | ? |
| 0 | 1 | 1 | ? | ? |
| 1 | 0 | 0 | ? | ? |
| 1 | 0 | 1 | ? | ? |
| 1 | 1 | 0 | ? | ? |
| 1 | 1 | 1 | ? | ? |
У нас есть три входные переменные: A, B и C. Запишем все возможные комбинации значений входных переменных в таблицу истинности и посчитаем значения функций f1 и f2 для каждой комбинации.
Для этого, давайте рассмотрим каждую функцию по отдельности:
Функция f1: f1 = A·(B̅+C)
Функция f2: f2 = A̅·(B̅+C̅)
Теперь, вставим значения функций в таблицу истинности:
| A | B | C | f1=A·(B̅+C) | f2=A̅·(B̅+C̅) |
|---|---|---|------------|--------------|
| 0 | 0 | 0 | ? | ? |
| 0 | 0 | 1 | ? | ? |
| 0 | 1 | 0 | ? | ? |
| 0 | 1 | 1 | ? | ? |
| 1 | 0 | 0 | ? | ? |
| 1 | 0 | 1 | ? | ? |
| 1 | 1 | 0 | ? | ? |
| 1 | 1 | 1 | ? | ? |
Теперь давайте пошагово рассчитаем значения функций для каждой комбинации входных переменных:
Для первой комбинации [A=0, B=0, C=0]:
f1 = 0 · (1 + 0) = 0 · 1 = 0
f2 = 0̅ · (1 + 0̅) = 1 · 1 = 1
Запишем значения в таблицу истинности:
| A | B | C | f1=A·(B̅+C) | f2=A̅·(B̅+C̅) |
|---|---|---|------------|--------------|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | ? | ? |
| 0 | 1 | 0 | ? | ? |
| 0 | 1 | 1 | ? | ? |
| 1 | 0 | 0 | ? | ? |
| 1 | 0 | 1 | ? | ? |
| 1 | 1 | 0 | ? | ? |
| 1 | 1 | 1 | ? | ? |
Продолжим аналогично для остальных комбинаций входных переменных:
[A=0, B=0, C=1]: f1 = 0 · (1 + 1) = 0 · 1 = 0, f2 = 1̅ · (1 + 1̅) = 1 · 1 = 1
[A=0, B=1, C=0]: f1 = 0 · (0 + 0) = 0 · 0 = 0, f2 = 1̅ · (0 + 0̅) = 1 · 0 = 0
[A=0, B=1, C=1]: f1 = 0 · (0 + 1) = 0 · 1 = 0, f2 = 1̅ · (0 + 1̅) = 1 · 1 = 1
[A=1, B=0, C=0]: f1 = 1 · (1 + 0) = 1 · 1 = 1, f2 = 0̅ · (1 + 0̅) = 0 · 1 = 0
[A=1, B=0, C=1]: f1 = 1 · (1 + 1) = 1 · 1 = 1, f2 = 0̅ · (1 + 1̅) = 0 · 1 = 0
[A=1, B=1, C=0]: f1 = 1 · (0 + 0) = 1 · 0 = 0, f2 = 0̅ · (0 + 0̅) = 0 · 1 = 0
[A=1, B=1, C=1]: f1 = 1 · (0 + 1) = 1 · 1 = 1, f2 = 0̅ · (0 + 1̅) = 0 · 0 = 0
Теперь, посмотрим на значения функций в таблице истинности:
| A | B | C | f1=A·(B̅+C) | f2=A̅·(B̅+C̅) |
|---|---|---|------------|--------------|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Как можем видеть из таблицы, значения функций f1 и f2 не совпадают для всех комбинаций входных переменных. Поэтому, булевые функции f1 и f2 не являются эквивалентными.