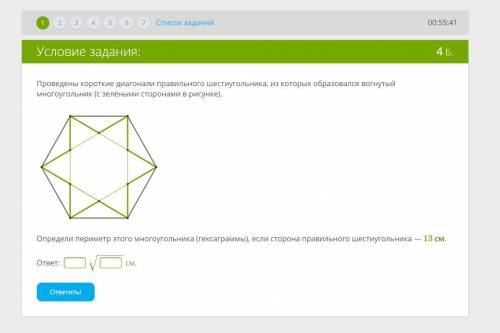
Проведены короткие диагонали правильного шестиугольника, из которых образовался вогнутый многоугольник (с зелёными сторонами в рисунке). Определи периметр этого многоугольника (гексаграммы), если сторона правильного шестиугольника - 13 см.

Для решения этой задачи, нам нужно определить периметр вогнутого многоугольника (гексаграммы), образованного короткими диагоналями правильного шестиугольника.

Для начала, нам нужно найти длину одной стороны вогнутого многоугольника. Мы знаем, что сторона правильного шестиугольника равна 13 см.

Теперь, если ты посмотришь на картинку, ты заметишь, что внутри шестиугольника образованы равносторонние треугольники.
Итак, один из этих треугольников с одной стороны соприкасается с диагоналями внутреннего многоугольника. Давай начнем с него.

Мы можем разделить этот треугольник на два прямоугольных треугольника. В каждом из них один из катетов (сторон, кроме гипотенузы) равен половине стороны внутреннего многоугольника, то есть 13 см / 2 = 6,5 см. Другой катет - это диагональ внутреннего многоугольника, для которого нам изначально не дана длина.

Применим теорему Пифагора к прямоугольному треугольнику: квадрат длины гипотенузы равен сумме квадратов длин катетов.
Таким образом, для каждого из двух прямоугольных треугольников мы можем записать формулу:
(длина диагонали)^2 = (6,5 см)^2 + (длина катета)^2

Теперь, давай найдем длину диагонали. Для этого нужно решить квадратное уравнение, использовав данную формулу.

(длина диагонали)^2 = (6,5 см)^2 + (длина катета)^2
(длина диагонали)^2 = (6,5 см)^2 + (13 см)^2
(длина диагонали)^2 = 42,25 см^2 + 169 см^2
(длина диагонали)^2 = 211,25 см^2

Теперь найдем квадратный корень из обеих сторон:

длина диагонали = √211,25 см
длина диагонали ≈ 14,54 см

Теперь мы знаем длину одной из диагоналей внутреннего многоугольника. Но внутри шестиугольника есть еще пять таких диагоналей, и все они равны между собой.

Таким образом, длина любой диагонали внутреннего многоугольника составляет около 14,54 см.

Теперь соберем обратно наш вогнутый многоугольник, используя данные о длине стороны правильного шестиугольника и длине диагонали внутреннего многоугольника.

Мы знаем, что внутренний многоугольник является равносторонним, поэтому его периметр равен 6 * длина стороны внутреннего многоугольника.

Периметр внутреннего многоугольника = 6 * 14,54 см
Периметр внутреннего многоугольника ≈ 87,24 см

Таким образом, периметр вогнутого многоугольника (гексаграммы) составляет около 87,24 см.