1. Математика
  2. Производная функции z = x 2

Производная функции z = x 2 y в точке Р (1; 0) в направлении вектора a = 3 i + 4 j равна

mssuslova1980 mssuslova1980    3   08.01.2021 12:47    0

Ответы
Kirill7692 Kirill7692  07.02.2021 12:48

Пошаговое объяснение:

z = yx²;   P(1;0);   a=3i + 4j

производная в точке P(1;0) по направлению вектора а(3;4).

∂z/∂a=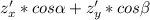  z'_x*cos\alpha +z'_y*cos\beta

z'_x=2xy;   z'_y=x^2

z'_x_{(1;0)}= 2*1*0=0;   z'_y_{(1;0)}=1^2=1

cos\alpha =\frac{x}{IaI;}   cos\beta = \frac{y}{IaI}

IaI = \sqrt{x^2+y^2} =\sqrt{3^2+4^2} =5

cos\alpha = 3/5;     cos\beta = 4/5

∂z/∂a = 0*(3/5) + 1* (4/5) = 4/5

∂z/∂a < 0, значит  заданная функция в направлении вектора a убывает.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
dinonafrie1488 dinonafrie1488  30.06.2019 19:50
Толкование пословиц в хорошей семье хорошие дети растут родня до полдня, а пообедать негде...
Белыйснег35 Белыйснег35  30.06.2019 19:50
Найдите среднее арифметическое корней уравнения: х(х-5,2)(3,4+х)(2,4-2х)=0 ответ: 0,75, подобрать решение: )...
Загадака Загадака  30.06.2019 19:50
Выполните действия: 1) (12,33+7,3): 6,5; 2) (6-2,43): 4 1/4; 3) 9,75: (4 1/2-2,55); 4) 15,96: (9/25+2,04; 5) (4 1/5-3,93): 4,5; 6) 1: (0,54+1,96); 7) 5,18: (5,13-3,65);...
Никита0897882969 Никита0897882969  30.06.2019 19:50
Решите в системе 3х^2+у=4 2х^2-у=1...
astahovanadezh astahovanadezh  30.06.2019 19:50
Зделайте 100 примеров на умнофение много...
DAYH228 DAYH228  30.06.2019 19:50
Нам задали вапрос такой: прямоугольный параллепипед ширеной 4 дм и высатой 6 дм имеет объём 216 дм в кубе. найдите периметер его наибольшей части...
karinka20001202 karinka20001202  30.06.2019 19:50
1вычислите ctg750 2.найдите наименьшее значение функции y=2x,если график первообразной проходит через точку (5; 2) 3.вычислите площадь фигуры,ограниченной линиями...
georgiy19971 georgiy19971  30.06.2019 19:50
Решите ширина прямоугольного паралепипеда равна 4.8 см что состовляет 12 пятнадцатых его длины а высота состовляет 25% длины вычеслить объём паралепипеда...
Elnura85 Elnura85  30.06.2019 19:50
Построить прямоугольник по заданным координатам.прямоугольник kmnp k(-1; 3) m(3; 3) n(3; -5) p(-1; -5).найдите координаты точки пересмечения диагоналей?...
bestaminova111 bestaminova111  30.06.2019 19:50
Ане, оле и юле нужно было закрасить третью часть прямоугольника. кто из детей выполнил верно?...

Популярные вопросы