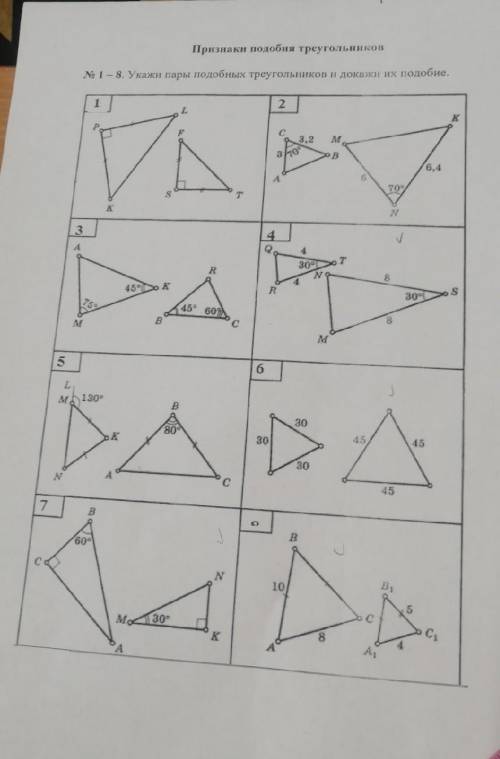
Признаки подобия треугольников номер 1-8. Укажите подобия треугольников и докажите их подобие​

Пошаговое объяснение:

Смотри по углам, если они. Сходятся значит они подобные,

5

Пошаговое объяснение:

потому что

Перед тем, как приступить к доказательству подобия треугольников, давайте сначала определимся с тем, что такое подобные треугольники.

Два треугольника считаются подобными, если соответствующие их углы равны, то есть угол треугольника А равен углу треугольника В, угол треугольника B равен углу треугольника В и угол треугольника С равен углу треугольника D. Помимо этого, их соответствующие стороны пропорциональны, то есть каждая сторона треугольника А соотносится с каждой соответствующей стороной треугольника В в одном и том же отношении.

Теперь рассмотрим каждую пару треугольников и доказательства их подобия:

1) Треугольники АВС и АDE:
Соответствующие углы: ∠А = ∠А (они равны, так как это одинаковые углы)
Соотношение сторон: AB/AD = AC/AE = BC/DE (соответственно стороны треугольников пропорциональны)

2) Треугольники АСВ и АDЕ:
Соответствующие углы: ∠В = ∠Е (они равны, так как это одинаковые углы)
Соотношение сторон: AC/AD = BC/BE (соответственно стороны треугольников пропорциональны)

3) Треугольники AСВ и ADE:
Соответствующие углы: ∠С = ∠D (они равны, так как это одинаковые углы)
Соотношение сторон: AB/AE = BC/DE (соответственно стороны треугольников пропорциональны)

4) Треугольники ВСМ и DEK:
Соответствующие углы: ∠ВСМ = ∠DEK (они равны, так как это одинаковые углы)
Соотношение сторон: ВС/DE = СМ/DK (соответственно стороны треугольников пропорциональны)

5) Треугольники ВКМ и DMН:
Соответствующие углы: ∠К = ∠Н (они равны, так как это одинаковые углы)
Соотношение сторон: VK/DM = КМ/НМ (соответственно стороны треугольников пропорциональны)

6) Треугольники AMK и DAN:
Соответствующие углы: ∠А = ∠А (они равны, так как это одинаковые углы)
Соотношение сторон: AK/AD = КМ/НМ (соответственно стороны треугольников пропорциональны)

7) Треугольники АCK и АHM:
Соответствующие углы: ∠К = ∠Н (они равны, так как это одинаковые углы)
Соотношение сторон: AK/AM = CK/HM (соответственно стороны треугольников пропорциональны)

8) Треугольники АВК и АМН:
Соответствующие углы: ∠В = ∠М (они равны, так как это одинаковые углы)
Соотношение сторон: AK/AM = BK/NМ (соответственно стороны треугольников пропорциональны)

Таким образом, мы доказали подобие всех пар треугольников, так как их углы равны и соответствующие стороны пропорциональны.