Приветики, объясните этот пример с частной производной А именно: почему если " Y"есть константа, то случаи с моим примером, оно записано как 6x^2y тогда почему "Y" добавлена в конце, разве она не равна = 0

А во втором случаи, когда "X" есть константа, то записано 2x^3 и почему здесь "Y" не записан тогда ? а два икс в кубе не равно нулю ?

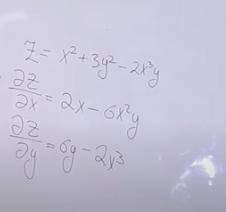
Приветики, объясните этот пример с частной производной А именно: почему если Yесть

Ответы

LarzMarz 15.10.2020 15:13

$z=x^2+3y^2-2x^3y\\\\\\\dfrac{\partial z}{\partial x}=\ \Big(y=const,\ C'=0\ ,\ (C\cdot x)'=C\cdot x'=C\cdot 1=C\Big)=\\\\=\Big(x^2+\underbrace {3y^2}_{C'=0}-2x^3\cdot \underbrace {y}_{C}\Big)'_{x}=2x+0-2y\cdot (x^3)'=2x-2y\cdot 3x^2=\\\\=2x-6x^2y\\\\\\\dfrac{\partial z}{\partial x}=\Big(x=const\Big)=\Big(\underbrace {x^2}_{C'=0}+3y^2-\underbrace {2x^3}_{C}y\Big)'_{y}=0+3\cdot 2y-2x^3\cdot y'=\\\\=6y-2x^3\cdot 1=6y-2x^3$

ПОКАЗАТЬ ОТВЕТЫ

МариКэт1 15.10.2020 15:13

Потому что константа не стоит одиноко, а составляет компанию двум иксам в кубе. Давайте по аналогии с производной для одной переменной. возьмем константу. ну ... например, ) 5.

5'=0

однако же..

(5x²)'=5*(x²)'=5*2х=10х, здесь не возникает вопросов, почему она не равна нулю? Отнеситесь к ней, как к обычному числу, т.е. дифференцируете по х, у константа, по у, х константа, т.е. число.

Во втором случае, по той же причине. 2x^3 - это константа, но рядом с ней у, константу выносим за знак производной, а производная у по у равна единице, умножили на константу, ее и получили.

Вот если бы Вы брали вторую частную производную по иксу во втором примере, тогда бы 6у обратился в нуль. т.к. производная чистой константы равна нулю.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика