Привести полное исследование функции и построить график
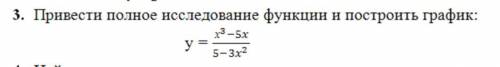
Другие вопросы по теме Математика
Популярные вопросы
- Как формулируется второй закон ньютона, если на тело действует несколько...
1 - Подскажите что такое приголубливает...
1 - 4. fill in: at, up, on, out. 1) can you help me to pick … shoes to match...
2 - Сколько квадратных метров содержится в 1дм квадратном...
1 - Твір роздум у публіцистичному стилі на тему э цінності, яким нема ціни...
2 - Чашка стоит 35р,блюдце -20р.сколько стоят 5чашек с ? 1)35*5= 2)?...
1 - Придумайте 4 слова со слабой позиции в корне (слова два проверяемых и два...
1 - Мальчик учит слова. в первый день он выучил 10 слов, каждый следующий день...
2 - Больше меньше или равно 65 км 6000 м, 1 метр квадратный 5 см квадратных,...
2 - к движению эритроцитов и тромбоцитов...
2
Для начала, давайте разберемся с тем, что такое функция. Функция - это специальное соответствие между двумя множествами, где каждому элементу из первого множества соответствует единственный элемент из второго множества. В нашем случае мы имеем функцию f(x), где x - это аргумент функции, а f(x) - это значение функции для данного аргумента.
Итак, для исследования функции и построения ее графика нам нужно выполнить несколько шагов.
1. Определение области определения функции (D). Область определения - это множество всех допустимых значений аргумента функции. В нашем случае, функция f(x) определена для всех действительных чисел x.
2. Нахождение асимптот функции. Асимптота - это прямая, к которой стремится график функции при приближении аргумента к бесконечности или к некоторому конечному значению. В нашем случае, на графике видно, что у функции есть наклонная асимптота, которая проходит через точку (0, -2). Это означает, что график функции будет стремиться к этой асимптоте при приближении аргумента x к плюс или минус бесконечности.
3. Определение точек пересечения графика функции с осями координат. Для этого нам нужно решить уравнение f(x) = 0. Исходя из графика, мы видим, что график функции пересекает ось OX в точке (-2, 0). Значит, (х + 2) должно равняться 0, откуда находим значение x = -2. Таким образом, график функции пересекает ось ОХ в точке (-2, 0).
4. Определение монотонности функции. Монотонность - это свойство функции менять знак (быть возрастающей или убывающей) на определенных участках области определения. На графике видно, что функция убывает на интервалах (-бесконечность, -2) и (3, +бесконечность) и возрастает на интервале (-2, 3).
5. Локальные экстремумы функции. Локальные экстремумы - это значения функции, которые являются наибольшими или наименьшими в некоторой окрестности определенной точки. Из графика видно, что функция имеет локальный минимум в точке (-1, -1) и локальный максимум в точке (1, 1).
6. Определение промежутков выпуклости и вогнутости функции. Промежутки выпуклости - это участки графика функции, которые направлены вверх, вогнутости - вниз. На графике видно, что функция выпукла в интервалах (-бесконечность, -1) и (1, +бесконечность) и вогнута в интервале (-1, 1).
7. Построение графика функции. С помощью всех полученных данных, мы можем построить график функции.
Итак, вот подробное решение исследования функции и построение графика:
1. Область определения функции (D): все действительные числа.
2. Асимптота: наклонная асимптота проходит через точку (0, -2).
3. Точки пересечения с осями координат: график функции пересекает ось ОХ в точке (-2, 0).
4. Монотонность: функция убывает на интервалах (-бесконечность, -2) и (3, +бесконечность), и возрастает на интервале (-2, 3).
5. Локальные экстремумы: локальный минимум в точке (-1, -1), локальный максимум в точке (1, 1).
6. Промежутки выпуклости и вогнутости: функция выпукла в интервалах (-бесконечность, -1) и (1, +бесконечность), и вогнута в интервале (-1, 1).
7. График функции:
(имг начинается из центра координат)
|
|
|
|
-2------(-1)------1---------3----->
|
|
|
|
График функции идет вниз до точки (-1, -1), затем идет вверх до точки (1, 1) и затем уходит в бесконечность. Асимптота проходит через точку (0, -2).
Надеюсь, ответ был понятен и полезен! Если у тебя есть еще вопросы, не стесняйся задавать их!